Usuario:
Vapor de Agua en el Suelo
Storyboard 
Normalmente la presión del vapor de agua real es menor que la máxima que soporta del aire antes de comenzar a condensarse este. Por ello se introduce el concepto de humedad relativa.
ID:(377, 0)
Fase gaseosa, vapor de agua
Concepto
La fase gaseosa, que en nuestro caso corresponde al vapor de agua, es aquella en la que los átomos pueden desplazarse relativamente libremente.
En esta fase, existe una interacción mínima que puede afectar el comportamiento de los átomos sin confinarlos de manera significativa.
ID:(15142, 0)
Fase liquida, agua
Concepto
La fase líquida, que en nuestro caso corresponde al agua, es aquella en la que los átomos pueden desplazarse relativa y libremente, manteniendo su unidad pero adaptándose a la forma que los contiene.
En esta fase, no se observa ninguna estructura definida.
ID:(15140, 0)
Fase solida, hielo
Concepto
La fase sólida, que en nuestro caso corresponde al hielo, es aquella en la que los átomos no pueden desplazarse relativamente y solo pueden oscilar en torno a su punto de equilibrio.
En esta fase, se puede observar una estructura que suele ser cristalina y, por lo tanto, regular.
ID:(15141, 0)
Diagrama de fase del agua
Concepto
Uno de los diagramas de fase más significativos para nuestro planeta es el del agua. Este diagrama presenta las tres fases clásicas: sólido, líquido y gas, además de una variedad de fases con diferentes estructuras cristalinas del hielo.
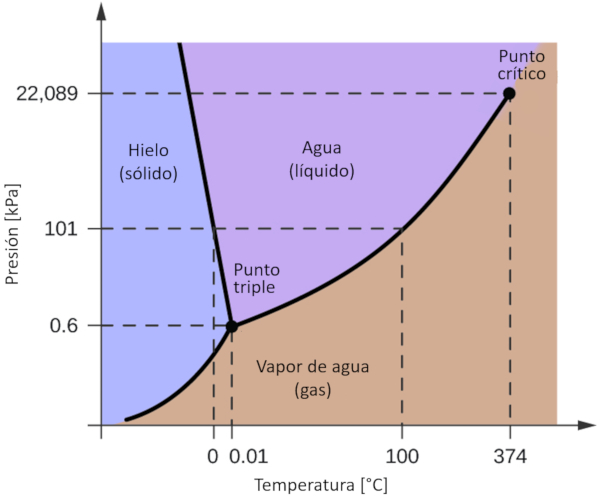
La característica más destacada en comparación con otros materiales es que en un rango de presión comprendido entre 611 Pa y 209.9 MPa, el estado sólido ocupa un volumen mayor que el estado líquido. Este fenómeno se refleja en el diagrama de fase como una pendiente negativa en la línea que separa las fases sólidas (hielo con estructura hexagonal) y líquidas (agua).
ID:(836, 0)
Medición de calor de evaporación
Imagen
La medición del calor de evaporación se realiza calentando una muestra, lo que provoca su evaporación, mientras se registra la cantidad de calor suministrada a la muestra. Luego, se enfría el vapor generado y se lo hace condensar, midiendo la masa originalmente evaporada.
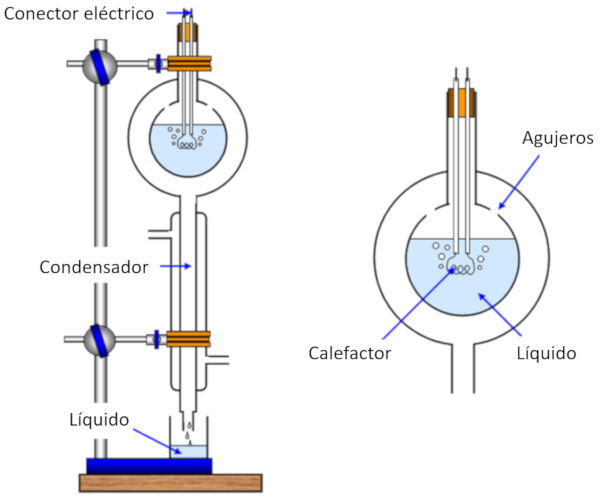
De esta manera, podemos calcular la energía necesaria para evaporar una masa determinada, lo que se expresa como calor latente ($L$) y se mide en julios por kilogramo (J/kg) o julios por mol (J/mol).
ID:(1662, 0)
Vapor de agua
Concepto
La fase gaseosa del agua corresponde a lo que se denomina el vapor de agua. Esta se crea cuando las moléculas de agua adquieren suficiente energía cinética para escapar de la fase líquida y comienzan a moverse en el espacio sobre el líquido. Periódicamente, las moléculas en estado gaseoso chocan nuevamente contra la superficie del líquido y son capturadas, volviendo al estado líquido.
A medida que aumenta el número de moléculas en estado gaseoso, también aumenta el número de moléculas que regresan al estado líquido. Este proceso continúa hasta que se alcanza un equilibrio entre las moléculas que abandonan el líquido y las que son reabsorbidas. En esta situación, se dice que el espacio sobre el líquido está saturado.
ID:(1010, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ dG =- S dT + V dp $
dG =- S * dT + V * dp
$ dH = T dS + V dp $
dH = T * dS + V * dp
$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$
dp / dT = L /( DV * T )
$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$
dp / dT = l_m /( Dv_m * T )
$ \delta Q = T dS $
dQ = T * dS
$ dU = \delta Q - \delta W $
dU = dQ - dW
$ dU = T dS - p dV $
dU = T * dS - p * dV
$ \delta W = p dV $
dW = p * dV
$ H = U + p V $
H = U + p * V
$ l_m \equiv\displaystyle\frac{ L }{ M_m }$
l_m = L / M_m
$ p = c_m R T $
p = c_m * R * T
$ p_s = p_{ref} e^{- l_m / R T }$
p_s = p_ref *exp(- l_m / R * T )
$ RH =\displaystyle\frac{ c_v }{ c_s }$
RH = c_v / c_s
$ RH =\displaystyle\frac{ p_v }{ p_s }$
RH = p_v / p_s
ID:(15231, 0)
Primera ley de la termodinámica
Ecuación
El diferencial de la energía interna ($dU$) siempre es igual a la cantidad de el diferencial inexacto del calor ($\delta Q$) suministrada al sistema (positiva) menos la cantidad de el diferencial inexacto del trabajo ($\delta W$) realizada por el sistema (negativa):
| $ dU = \delta Q - \delta W $ |
ID:(9632, 0)
Trabajo en función del volumen
Ecuación
En analogía con la definición del trabajo $dW$ en la mecánica:
| $ \delta W = F dx $ |
que se define en función de la fuerza $F$ y el desplazamiento $dx$, en termodinámica se trabaja con la expresión del trabajo en función de la presión $p$ y la variación de volumen $dV$:
| $ \delta W = p dV $ |
Como el trabajo se define como la fuerza por el camino recorrido
| $ \delta W = F dx $ |
se tiene que si multiplicamos y dividimos por una sección $S$
$\delta W = \displaystyle\frac{F}{S}Sdz$
se puede reemplazar el primer termino con la presión
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y el elemento de volumen
| $ \Delta V = S \Delta s $ |
con lo que el trabajo en función de presión y volumen es
| $ \delta W = p dV $ |
ID:(9634, 0)
Segunda ley de la termodinámica
Ecuación
El diferencial inexacto del calor ($\delta Q$) es igual a la temperatura absoluta ($T$) por la variación de la entropía ($dS$):
| $ \delta Q = T dS $ |
ID:(9639, 0)
Energía Interna: relación diferencial
Ecuación
La dependencia de el diferencial de la energía interna ($dU$) de la presión ($p$) y la variación del volumen ($dV$), además de la temperatura absoluta ($T$) y la variación de la entropía ($dS$), está dada por:
| $ dU = T dS - p dV $ |
Dado que el diferencial de la energía interna ($dU$) depende de el diferencial inexacto del calor ($\delta Q$), la presión ($p$) y la variación del volumen ($dV$) según la ecuación:
| $ dU = \delta Q - p dV $ |
y la expresión de la segunda ley de la termodinámica con la temperatura absoluta ($T$) y la variación de la entropía ($dS$) como:
| $ \delta Q = T dS $ |
podemos concluir que:
| $ dU = T dS - p dV $ |
.
ID:(3471, 0)
Entalpia
Ecuación
La entalpía ($H$) se define como la suma de la energía interna ($U$) y la energía de formación. Esta última corresponde al trabajo realizado en la formación, que es igual a $pV$ con la presión ($p$) y el volumen ($V$). Por lo tanto, obtenemos:
| $ H = U + p V $ |
ID:(3536, 0)
Relación diferencial de la Entalpía
Ecuación
La dependencia de el diferencial de la entalpía ($dH$) de la temperatura absoluta ($T$) y la variación de la entropía ($dS$), además de el volumen ($V$) y la variación de la presión ($dp$), está dada por:
| $ dH = T dS + V dp $ |
Si se diferencia la definición de la entalpía ($H$), que depende de la energía interna ($U$), la presión ($p$) y el volumen ($V$), según
| $ H = U + p V $ |
se obtiene:
$dH = dU + Vdp + pdV$
con el diferencial de la entalpía ($dH$), el diferencial de la energía interna ($dU$), la variación de la presión ($dp$) y la variación del volumen ($dV$).
Con el diferencial de la energía interna ($U$) respecto a la temperatura absoluta ($T$) y la entropía ($S$),
| $ U = T S - p V $ |
se obtiene:
| $ dU = T dS - p dV $ |
con el diferencial de la energía interna ($dU$) y la variación de la entropía ($dS$).
Finalmente, se concluye que:
| $ dH = T dS + V dp $ |
ID:(3473, 0)
Energía libre de Gibbs como diferencial
Ecuación
La dependencia de la variación de la Energía Libre de Gibbs ($dG$) de la entropía ($S$) y la variación de la temperatura ($dT$), además de el volumen ($V$) y la variación de la presión ($dp$), está dada por:
| $ dG =- S dT + V dp $ |
La energía libre de Gibbs ($G$) en función de la entalpía ($H$), la entropía ($S$) y la temperatura absoluta ($T$) se expresa de la siguiente manera:
| $ G = H - T S $ |
El valor de el diferencial de la energía libre de Gibbs ($dG$) se calcula utilizando el diferencial de la entalpía ($dH$), la variación de la temperatura ($dT$) y la variación de la entropía ($dS$) mediante la ecuación:
$dG=dH-SdT-TdS$
Dado que el diferencial de la entalpía ($dH$) está relacionado con el volumen ($V$) y la variación de la presión ($dp$) de acuerdo con:
| $ dH = T dS + V dp $ |
Se deduce que el diferencial de la entalpía ($dH$), la variación de la entropía ($dS$) y la variación de la presión ($dp$) están interrelacionados de la siguiente manera:
| $ dG =- S dT + V dp $ |
ID:(3541, 0)
Ley de Clausius Clapeyron
Ecuación
La ley de Clausius-Clapeyron establece una relación entre la variación de la presión ($dp$) y la variación de la temperatura ($dT$) con el calor latente ($L$), la temperatura absoluta ($T$) y la variación de volumen en cambio de fase ($\Delta V$) de la siguiente manera:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
Si el diferencial de la energía libre de Gibbs ($dG$) es constante, esto significa que para la variación de la presión ($dp$) y la variación de la temperatura ($dT$), el valor de la entropía ($S$) y el volumen ($V$) en la fase 1
$dG = -S_1dT+V_1dp$
y la entropía ($S$) y el volumen ($V$) en la fase 2
$dG = -S_2dT+V_2dp$
resultan en
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
El cambio en la entropía ($S$) entre ambas fases corresponde a el calor latente ($L$) dividido por la temperatura absoluta ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Entonces, con la definición de la variación de volumen en cambio de fase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
obtenemos
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
ID:(12824, 0)
Conversión calor latente molar
Ecuación
En muchas ocasiones, no se dispone del calor latente molar, sino del calor latente que se expresa, por ejemplo, en Joules por kilogramo (J/kg). Dado que la ecuación de presión de vapor trabaja con el calor latente molar, es necesario convertir el calor latente en calor latente molar. Como este último se refiere a la cantidad por mol, simplemente dividimos el calor latente ($L$) por la masa molar ($M_m$) para obtener el calor latente molar ($l_m$):
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
En el caso del agua, el calor latente de evaporación es del orden de $L\sim 2.256\times 10^6 J/kg$, mientras que la masa molar es $M_m\sim 18 g/cm^3 = 0.018 kg/m^3$. De esta manera, obtenemos un calor latente molar de $L_m\sim 40600 J/mol = 40.6 kJ/mol$.
ID:(9273, 0)
Ley de Clausius Clapeyron molar
Ecuación
La ecuación de Clausius-Clapeyron establece una relación entre la variación de la presión ($dp$) y la variación de la temperatura ($dT$) con la temperatura absoluta ($T$), el calor latente molar ($l_m$) y el variación del volumen molar en cambio de fase ($\Delta v_m$) de la siguiente manera:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
Con la ley de Clausius-Clapeyron, que depende de la variación de la presión ($dp$), la variación de la temperatura ($dT$), el calor latente ($L$), la variación de volumen en cambio de fase ($\Delta V$) y la temperatura absoluta ($T$) y se expresa como:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
y la definición de el calor latente molar ($l_m$), en la que el calor latente ($L$) está relacionado con la masa molar ($M_m$) de la siguiente manera:
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
y el variación del volumen molar en cambio de fase ($\Delta v_m$), en la que la variación de volumen en cambio de fase ($\Delta V$) está relacionado con la masa molar ($M_m$) de la siguiente manera:
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
se obtiene:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
ID:(12822, 0)
Cantidad de vapor de agua
Concepto
La variación de volumen en cambio de fase ($\Delta V$), al cambiar de fase de un líquido a un gas, se puede expresar como:
$\Delta V = V_{\text{gas}} - V_{\text{líquido}}$
Dado que el volumen del gas es significativamente mayor que el del líquido,
$V_{\text{gas}} \gg V_{\text{líquido}}$
podemos aproximar:
$\Delta V \approx V_{\text{gas}}$
Debido a que el vapor de agua exhibe un comportamiento similar al de un gas ideal, podemos afirmar que con los valores de la constante universal de los gases ($R$), el número de moles ($n$), la temperatura absoluta ($T$) y la presión de vapor de agua no saturado ($p_v$):
por lo que la variación de volumen en cambio de fase ($\Delta V$) es
$\Delta V = \displaystyle\frac{nRT}{p_v}$
ID:(3185, 0)
Presión de vapor de agua saturado
Ecuación
La presión de vapor de agua saturado ($p_s$) se puede calcular utilizando la presión de referencia ($p_{ref}$), la constante universal de los gases ($R$), la temperatura absoluta ($T$) y el calor latente molar ($l_m$) de acuerdo con la siguiente fórmula:
| $ p_s = p_{ref} e^{- l_m / R T }$ |
Utilizando la ecuación de Clausius-Clapeyron para el gradiente de la presión ($p$) en relación con la temperatura absoluta ($T$), que depende de el calor latente ($L$) y la variación de volumen en cambio de fase ($\Delta V$):
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
En el caso del cambio de fase de líquido a gas, podemos suponer que el cambio de volumen es aproximadamente igual al volumen del vapor, por lo que podemos utilizar la ecuación de los gases con el número de moles ($n$), el volumen ($V$), la constante universal de los gases ($R$) y la presión de vapor de agua no saturado ($p_v$):
| $$ |
Dado que la ecuación de Clausius-Clapeyron se puede expresar como:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Donde el calor latente molar ($l_m$) ($l_m = L/n$) representa el cambio de entalpía en el cambio de fase $\Delta h$ (la energía necesaria para formar el agua), finalmente obtenemos:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Si integramos esta ecuación entre la presión de vapor de agua saturado ($p_s$) y la presión en el punto
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Si evaluamos esta expresión con los datos del punto crítico:
$p_{ref}=p_0e^{l_m/RT_0}$
Finalmente, tenemos:
| $ p_s = p_{ref} e^{- l_m / R T }$ |
ID:(3182, 0)
Humedad relativa, concentración
Ecuación
La relación entre la concentración de moleculas de vapor de agua ($c_v$) y concentración de vapor de agua saturado ($c_s$) se llama la humedad relativa ($RH$). En otras palabras, cuando se alcanza una humedad relativa del 100%, la concentración existente será igual a la concentración saturada.
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
ID:(3175, 0)
Presión en función de la concentración molar
Ecuación
La presión ($p$) se puede calcular a partir de la concentración molar ($c_m$) utilizando la temperatura absoluta ($T$) y la constante universal de los gases ($R$) de la siguiente manera:
| $ p = c_m R T $ |
Cuando la presión ($p$) se comporta como un gas ideal, cumpliendo con el volumen ($V$), el número de moles ($n$), la temperatura absoluta ($T$) y la constante universal de los gases ($R$), la ecuación de los gases:
| $ p V = n R T $ |
y la definición de la concentración molar ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
llevan a la siguiente relación:
| $ p = c_m R T $ |
ID:(4479, 0)
Humedad relativa
Ecuación
La humedad relativa ($RH$) se puede expresar en términos de la presión de vapor de agua no saturado ($p_v$) y la presión de vapor de agua saturado ($p_s$) de la siguiente manera:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
La relación entre la humedad relativa ($RH$) con la concentración de moleculas de vapor de agua ($c_v$) y concentración de vapor de agua saturado ($c_s$) se expresa como:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
y relacionando la presión ($p$) con la concentración molar ($c_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R$) se obtiene:
| $ p = c_m R T $ |
Esto se aplica a la presión de vapor de agua, donde:
$p_v = c_v R T$
y a la presión saturada de vapor de agua:
$p_s = c_s R T$
Lo que resulta en la siguiente ecuación:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
ID:(4478, 0)