Usuario: 
Transporte de calor
Storyboard 
La humedad en el suelo está estrechamente relacionada con su temperatura, por lo que resulta crucial calcular esta distribución. Esta relación se establece en función del flujo de calor que se transporta hacia o desde la superficie del suelo.
ID:(2054, 0)
Mecanismo de transporte de calor
Top
En el caso de un sólido, y de manera similar para un líquido, podemos describir el sistema como una estructura de átomos unidos por algo que se comporta como un resorte. Cuando ambos extremos tienen valores de temperatura de una diferencia de temperatura en el conductor ($\Delta T_0$), siendo la temperatura en la superficie interior ($T_{is}$) y la temperatura en la superficie exterior ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
La diferencia en temperaturas implica que los átomos en los extremos oscilan de manera distinta; los átomos en la zona de alta temperatura tendrán una amplitud mayor en sus oscilaciones en comparación con los átomos en la zona de baja temperatura.
Sin embargo, esta diferencia llevará gradualmente a que toda la cadena oscile de tal manera que, al final, la amplitud variará a lo largo del camino, desde los valores más altos donde la temperatura también es mayor, hasta los valores más bajos en la zona de menor temperatura.
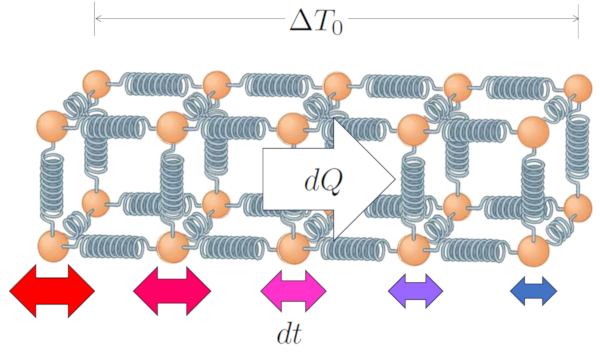
De esta manera, la diferencia de temperatura en el conductor ($\Delta T_0$) conduce a una calor transportado ($dQ$) en una variación de tiempo ($dt$).
ID:(15234, 0)
Dependencia de la geometría y el material
Top
Uno de los factores clave que determina cuánto calor puede ser conducido a través de un sólido o líquido es su sección transversal, es decir, la cantidad de cadenas de átomos disponibles. Cuantas más de estas cadenas tengamos, mayor será nuestra capacidad de transporte de calor.
Sin embargo, la longitud de las cadenas puede ser contraproducente. A medida que la cadena de resortes se vuelve más larga, nuestra capacidad de transmitir calor disminuye, ya que más átomos deben modificar su amplitud de oscilación.
Si representamos esto con la sección ($S$) y el largo del conductor ($L$), el diagrama adquirirá la siguiente forma:
Finalmente, la capacidad de los medios y del material para transportar el calor, que se describen mediante la conductividad térmica ($\lambda$), explica cómo el calor se desplaza ante la diferencia de temperatura ($\Delta T$) transportanto la calor transportado ($dQ$) en la variación de tiempo ($dt$):
ID:(15235, 0)
Conducción de calor
Top
La conducción de calor fue modelada por primera vez por Jean Baptiste Joseph Fourier [1], quien estableció que la tasa de flujo de calor ($q$), definido mediante la calor transportado ($dQ$), la variación de tiempo ($dt$) y la sección ($S$), se expresa a través de:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
Esta teoría también se relaciona con la sección ($S$), el largo del conductor ($L$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la conductividad térmica ($\lambda$), como se muestra en:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
y se ilustra mediante el siguiente diagrama:
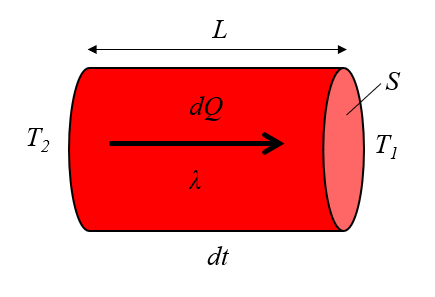
[1] "Théorie Analytique de la Chaleur" (La Teoría Analítica del Calor), Jean Baptiste Joseph Fourier, 1822.
ID:(15236, 0)
Dependencia de la transmisión de calor de la geometría al conductor
Top
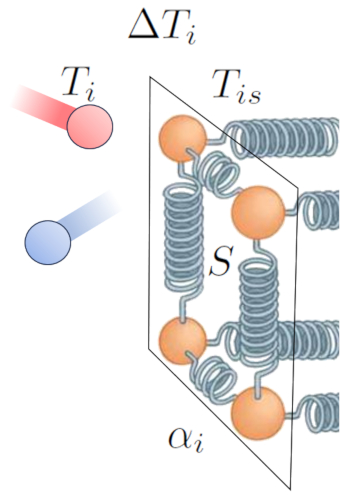
El principal impulsor de la transferencia de calor desde un medio a un conductor es la diferencia de temperatura. Cuando en el medio la temperatura en el interior ($T_i$), las partículas poseen más energía y al chocar con las del conductor a una temperatura en la superficie interior ($T_{is}$), tienden a aumentar la energía de este último. Esta interacción se puede representar de la siguiente manera:
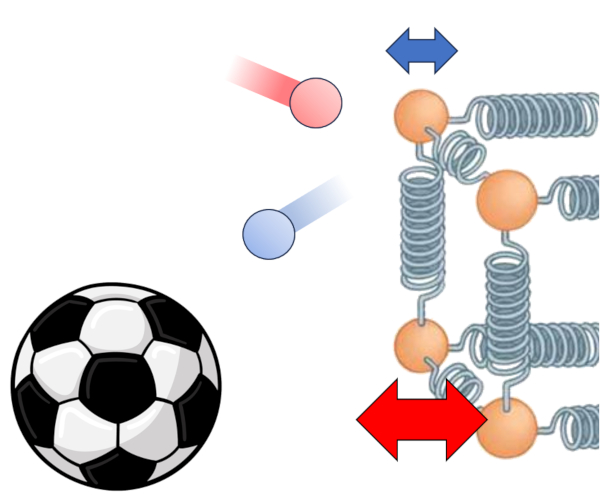
Además de la temperatura en sí, el flujo de calor depende de la diferencia de temperatura en interfaz interna ($\Delta T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
Otro factor clave es el número de átomos a los que se les puede aumentar la amplitud de la oscilación, lo cual depende de la sección ($S$). Por último, debemos considerar las propiedades de la superficie, que se describen mediante el coeficiente de transmisión interno ($\alpha_i$), que corresponde a la relación entre el calor transmitido, la superficie, la diferencia de temperatura y el tiempo transcurrido:
ID:(15237, 0)
Calculo de la transmisión de calor al conductor
Top
De esta forma, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de la diferencia de temperatura en interfaz interna ($\Delta T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
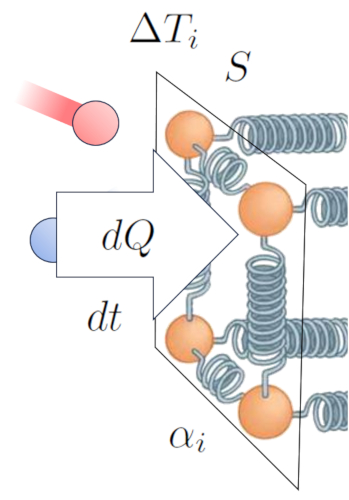
Esta expresión puede formularse matemáticamente de la siguiente manera:
| $ q = \alpha_i \Delta T_i $ |
ID:(15238, 0)
Dependencia de la transmisión de calor de la geometría desde el conductor
Top
El principal impulsor de la transferencia de calor desde un conductor hacia un medio es la diferencia de temperatura. Cuando la temperatura en la superficie exterior ($T_{es}$), las partículas tienen más energía y oscilan con una amplitud mayor al interactuar con los átomos y moléculas del medio a una temperatura en el exterior ($T_e$). Esto tiende a aumentar la energía de estos últimos. Esta interacción se puede representar de la siguiente manera:
Además de la temperatura, el flujo de calor depende de la diferencia de temperatura en la interfaz externa ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Otro factor clave es el número de átomos que pueden tener aumentada su amplitud de oscilación, lo cual depende de la sección ($S$). Finalmente, debemos considerar las propiedades superficiales, representadas por el coeficiente de transmisión externo ($\alpha_e$), que corresponde a la relación entre el calor transmitido, el área superficial, la diferencia de temperatura y el tiempo transcurrido:
ID:(15239, 0)
Transmisión de calor desde el conductor
Top
De esta manera, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y el coeficiente de transmisión externo ($\alpha_e$):
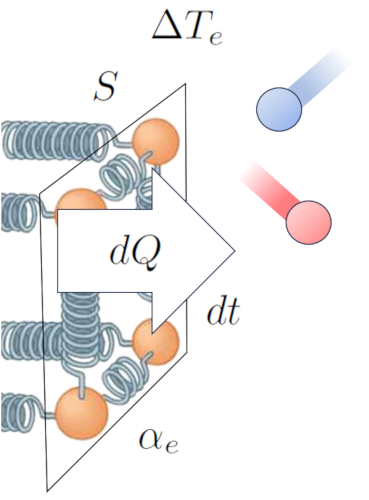
Matemáticamente, esto puede expresarse de la siguiente manera:
| $ q = \alpha_e \Delta T_e $ |
ID:(15240, 0)
Transporte total de calor por un conductor
Top
Los modelos de transferencia y conducción de calor sugieren que es posible desarrollar una relación que incorpore los tres mecanismos en conjunto. Esta ecuación deberá tener en cuenta la calor transportado ($dQ$), la variación de tiempo ($dt$), la diferencia de temperatura ($\Delta T$), la sección ($S$) y el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$):
Matemáticamente, esto se puede expresar de la siguiente manera:
| $ q = k \Delta T $ |
ID:(15241, 0)
Dependencia del coeficiente de transferencia de la velocidad del medio
Concepto
Uno de los efectos de la transferencia de calor de un conductor a un medio externo es el calentamiento del medio cercano a la interfaz, creando una zona de interferencia en la transmisión. Esto disminuye la eficiencia de la transferencia y tiende a formar una capa aislante que reduce el flujo de energía.
Sin embargo, este efecto puede modificarse en presencia de viento. El viento puede disipar la capa de átomos y moléculas a alta temperatura, aumentando la eficiencia de la transferencia de calor. Esto indica que el coeficiente de transmisión ($\alpha$) está influenciado por la velocidad del medio ($v_m$) [1,2]:
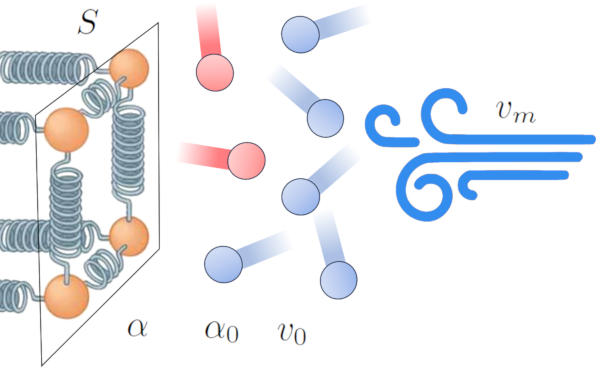
En este contexto, modelamos la relación en función de coeficiente de transmisión sin velocidad ($\alpha_0$) y un factor de referencia el velocidad de referencia del medio ($v_0$).
La relación matemática que describe este fenómeno para un gas con el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Y para un líquido con el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Esto demuestra cómo el viento puede afectar significativamente la eficiencia de la transferencia de calor entre un conductor y un medio externo.
[1] "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" (Sobre el movimiento de fluidos con muy poca fricción), Ludwig Prandtl, 1904
[2] "Die Abhängigkeit der Wärmeübergangszahl von der Rohrlänge" (La dependencia del coeficiente de transferencia de calor de la longitud del tubo), Wilhelm Nusselt, 1910
ID:(3620, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$
1/ k =1/ alpha_e + L / lambda
$\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$
1/ k =1/ alpha_i + 1/ alpha_e + L / lambda
$ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$
alpha_gv = alpha_g0 * (1+ v_m / v_g0 )
$ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$
alpha_wv = alpha_w0 * (1+sqrt( v_m / v_w0 ))
$ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $
DT = DT_i + DT_0 + DT_e
$ \Delta T = T_i - T_e $
DT = T_i - T_e
$ \Delta T_0 = T_{is} - T_{es} $
DT_0 = T_is - T_es
$ \Delta T_e = T_{es} - T_e $
DT_e = T_es - T_e
$ \Delta T_i = T_i - T_{is} $
DT_i = T_i - T_is
$ \lambda = \lambda_w^{\Phi} \lambda_b^{1-\Phi} e^{-\beta \Phi (1-\theta_S)^2}$
lambda = lambda_w ^ Phi * lambda_b ^(1- Phi )*exp(- beta * Phi *(1-theta_S )^2)
$ \lambda_b = \lambda_a g_a + \lambda_i g_i + \lambda_c g_c $
lambda_b = lambda_a * g_a + lambda_i * g_i + lambda_c * g_c
$ q = \alpha_e \Delta T_e $
q = alpha_e * DT_e
$ q = \alpha_i \Delta T_i $
q = alpha_i * DT_i
$ q = k \Delta T $
q = k * DT
$ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $
q = lambda * DT_0 / L
$ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $
T_es = T_e + k * DT / alpha_e
$ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $
T_is = T_i - k * DT / alpha_i
$\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$
1/ k =1/ alpha_i +1/ alpha_e +@SUM( L_i / lambda_i , i )
ID:(15229, 0)
Diferencia de temperatura superficial
Ecuación
En el caso de un sólido, y de manera similar para un líquido, podemos describir el sistema como una estructura de átomos unidos por algo que se comporta como un resorte. Cuando ambos extremos tienen valores de temperatura de una diferencia de temperatura en el conductor ($\Delta T_0$), siendo la temperatura en la superficie interior ($T_{is}$) y la temperatura en la superficie exterior ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
ID:(15120, 0)
Diferencia de temperatura
Ecuación
La diferencia de temperatura ($\Delta T$) se calcula restando la temperatura en el exterior ($T_e$) y la temperatura en el interior ($T_i$), lo cual se expresa de la siguiente manera:
| $ \Delta T = T_i - T_e $ |
ID:(15116, 0)
Calculo de la conducción de calor
Ecuación
El flujo de calor ($q$) es una función de la conductividad térmica ($\lambda$), el largo del conductor ($L$) y la diferencia de temperatura en el conductor ($\Delta T_0$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
ID:(7712, 0)
Diferencia de temperatura medio a conductor
Ecuación
La diferencia de temperatura en interfaz interna ($\Delta T_i$) se calcula restando la temperatura en la superficie interior ($T_{is}$) de la temperatura en el interior ($T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
ID:(15117, 0)
Calculo de la transmisión de calor al conductor
Ecuación
De esta forma, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de la diferencia de temperatura en interfaz interna ($\Delta T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
ID:(15113, 0)
Diferencia de temperatura conductor al medio
Ecuación
La diferencia de temperatura en la interfaz externa ($\Delta T_e$) se calcula restando la temperatura en la superficie exterior ($T_{es}$) de la temperatura en el exterior ($T_e$):
| $ \Delta T_e = T_{es} - T_e $ |
ID:(15118, 0)
Calculo de la transmisión de calor desde el conductor
Ecuación
De esta manera, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y el coeficiente de transmisión externo ($\alpha_e$):
| $ q = \alpha_e \Delta T_e $ |
ID:(15114, 0)
Cálculo del transporte total de calor por un conductor
Ecuación
De esta manera, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) y la diferencia de temperatura ($\Delta T$):
| $ q = k \Delta T $ |
Con la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$), la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y la diferencia de temperatura ($\Delta T$), obtenemos
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
que se puede reescribir con la calor transportado ($dQ$), la variación de tiempo ($dt$), la sección ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
y con la conductividad térmica ($\lambda$) y el largo del conductor ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
y
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
como
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
lo que resulta en
| $ q = k \Delta T $ |
ID:(7716, 0)
Variación total de la temperatura
Ecuación
En el proceso de transporte de calor, la temperatura disminuye gradualmente desde el sistema con mayor temperatura (interno) al de menor temperatura (externo). En este proceso, primero desciende desde la temperatura media interna hasta llegar a la diferencia de temperatura en interfaz interna ($\Delta T_i$), luego a la diferencia de temperatura en el conductor ($\Delta T_0$) y finalmente a la diferencia de temperatura en la interfaz externa ($\Delta T_e$). La suma de estas tres variaciones equivale a la caída total, es decir, la diferencia de temperatura ($\Delta T$), como se muestra a continuación:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Si se suman la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y se usan las ecuaciones
| $ \Delta T_i = T_i - T_{is} $ |
| $ \Delta T_0 = T_{is} - T_{es} $ |
y
| $ \Delta T_e = T_{es} - T_e $ |
se obtiene
$\Delta T_i + \Delta T_0 + \Delta T_e = T_i - T_e$
que con
| $ \Delta T = T_i - T_e $ |
resulta
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
ID:(15115, 0)
Constante de transporte total (un medio, dos interfaces)
Ecuación
El valor de el coeficiente de total de transporte ($k$) en la ecuación de transporte se determina utilizando el coeficiente de transmisión externo ($\alpha_e$), el coeficiente de transmisión interno ($\alpha_i$), la conductividad térmica ($\lambda$) y el largo del conductor ($L$) de la siguiente manera:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
Con la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$), la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y la diferencia de temperatura ($\Delta T$), obtenemos
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
que se puede reescribir con la calor transportado ($dQ$), la variación de tiempo ($dt$), la sección ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
y con la conductividad térmica ($\lambda$) y el largo del conductor ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
como
$\Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \displaystyle\frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right)$
por lo que podemos definir un coeficiente combinado como
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
ID:(3486, 0)
Temperatura en la superficie interna del conductor
Ecuación
La temperatura en la superficie interior ($T_{is}$) no es igual a la temperatura del medio, que es la temperatura en el interior ($T_i$). Esta temperatura se puede calcular a partir de la diferencia de temperatura ($\Delta T$), el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) y el coeficiente de transmisión interno ($\alpha_i$) mediante la siguiente fórmula:
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
Con la calor transportado ($dQ$), la variación de tiempo ($dt$), la sección ($S$), la diferencia de temperatura ($\Delta T$) y el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$), obtenemos
| $ q = k \Delta T $ |
que con el coeficiente de transmisión interno ($\alpha_i$) y la diferencia de temperatura en interfaz interna ($\Delta T_i$)
| $ q = \alpha_i \Delta T_i $ |
resulta en
$k\Delta T = \alpha_i \Delta T_i$
y con la temperatura en el interior ($T_i$) y la temperatura en la superficie interior ($T_{is}$) y
| $ \Delta T_i = T_i - T_{is} $ |
resulta en
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
ID:(15121, 0)
Temperatura en la superficie externa del conductor
Ecuación
La temperatura en la superficie exterior ($T_{es}$) no es igual a la temperatura del medio, que es la temperatura en el exterior ($T_e$). Esta temperatura se puede calcular a partir de la diferencia de temperatura ($\Delta T$), el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) y el coeficiente de transmisión externo ($\alpha_e$) utilizando la siguiente fórmula:
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
Con la calor transportado ($dQ$), la variación de tiempo ($dt$), la sección ($S$), la diferencia de temperatura ($\Delta T$) y el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$), obtenemos
| $ q = k \Delta T $ |
que, con el coeficiente de transmisión externo ($\alpha_e$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$)
| $ q = \alpha_e \Delta T_e $ |
resulta en
$k\Delta T = \alpha_e \Delta T_e$
y con la temperatura en el exterior ($T_e$) y la temperatura en la superficie exterior ($T_{es}$) y
| $ \Delta T_e = T_{es} - T_e $ |
resulta en
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
ID:(15122, 0)
Constante de transporte total (un medio, una interfaz)
Ecuación
El valor de el coeficiente de total de transporte ($k$) en la ecuación de transporte se determina utilizando el coeficiente de transmisión externo ($\alpha_e$), la conductividad térmica ($\lambda$) y el largo del conductor ($L$) de la siguiente forma:
| $ \displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
ID:(3619, 0)
Constante de transporte total (multiples medios, dos interfaces)
Ecuación
El valor de la tasa de flujo de calor ($q$) en la ecuación de transporte se determina utilizando el coeficiente de transmisión interno ($\alpha_i$), el coeficiente de transmisión externo ($\alpha_e$), la conductividad térmica elemento i ($\lambda_i$) y el largo elemento i ($L_i$) de la siguiente forma:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
ID:(7730, 0)
Constante de transferencia de calor en gas
Ecuación
Si un medio se desplaza con una constante de el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$) y la velocidad del medio ($v_m$) es igual a
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
donde el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) representa el caso en el que el medio no se desplaza y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es la velocidad de referencia.
La constante de transferencia térmica del material en el caso de un gas en reposo es de $5.6 J/m^2sK$, mientras que la velocidad de referencia es de $1.41 m/s$
ID:(7715, 0)
Constante de transferencia de calor en líquido
Ecuación
Si un medio se desplaza con una constante de el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$) y la velocidad del medio ($v_m$) es igual a
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
donde el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) representa el caso en el que el medio no se desplaza y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$) es la velocidad de referencia.
La constante de transferencia térmica del material para el caso de un líquido en reposo es igual a $340 J/m^2sK$, mientras que la velocidad de referencia es de $0.0278 m/s$.
ID:(7714, 0)
Conductividad térmica de suelo seco
Ecuación
La modelación de la conductividad térmica en un medio poroso como el suelo es un desafío. En este estudio, se llevaron a cabo análisis en una amplia variedad de muestras y se desarrolló un modelo numérico para predecir la conductividad térmica en el suelo seco ($\lambda_b$) en función de las texturas del suelo [1].
La relación de la conductividad térmica en el suelo seco ($\lambda_b$) se determinó en base a la conductividad térmica en arena ($\lambda_a$), la conductividad térmica en limo ($\lambda_i$), la conductividad térmica en arcilla ($\lambda_c$) y la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$), la fracción de masa de arcilla en la muestra ($g_c$), utilizando la siguiente fórmula:
| $ \lambda_b = \lambda_a g_a + \lambda_i g_i + \lambda_c g_c $ |
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Principios físicos y métodos de cálculo de la transferencia de humedad y calor en zanjas de cables.), Brakelmann, H., etz-Report 19, 93p. (1984), Berlin; Offenbach.
ID:(15130, 0)
Conductividad térmica de suelo con agua
Ecuación
El modelo de Brakelmann permite estimar la conductividad térmica en el suelo con agua ($\lambda$) con la conductividad térmica en el suelo seco ($\lambda_b$), la conductividad térmica en el agua ($\lambda_w$), la porosidad másica ($\Phi$), el saturación relativa másica ($\theta_S$) y el parámetro del Modelo de Brakelmann ($\beta$) mediante
| $ \lambda = \lambda_w^{\Phi} \lambda_b^{1-\Phi} e^{-\beta \Phi (1-\theta_S)^2}$ |
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Principios físicos y métodos de cálculo de la transferencia de humedad y calor en zanjas de cables.), Brakelmann, H., etz-Report 19, 93p. (1984), Berlin; Offenbach.
ID:(15131, 0)