Force de gravité et marées en opposition
Storyboard 
Une des accélérations à calculer est celle parallèle à l'écliptique (dans le plan Terre-corps céleste) en opposition, c'est-à-dire du côté opposé au corps céleste.
ID:(1575, 0)
Variation de la gravité parallèle au rayon, en opposition
Image 
L'attraction du côté opposé au corps céleste agissant sur la Terre est moindre en raison de la plus grande distance. Cela facilite le déplacement de l'eau vers l'équateur. D'autre part, du côté faisant face au corps céleste, son attraction affaiblit l'accélération gravitationnelle de la Terre, conduisant à une réduction de la gravité qui favorise davantage le déplacement de l'eau vers l'équateur :
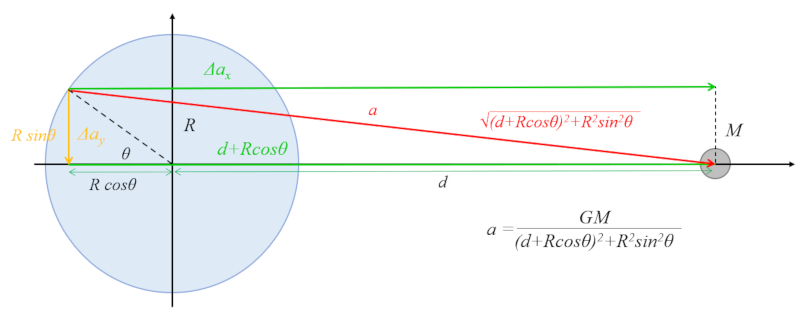
Dans ce cas, nous travaillons avec la similitude dans le triangle, où nous prenons la proportion
\Delta a_{ox}/a_o
et le cateto
d + R\cos\theta
et l'hypoténuse
(d+R\cos\theta)^2+R^2\sin^2\theta=d^2+R^2+2dR\cos\theta
ID:(11639, 0)
Explication intuitive de la marée du côté opposé du corps céleste
Image 
Il existe plusieurs explications possibles pour les marées du côté opposé du corps céleste. L'une d'entre elles est l'effet de l'accélération centrifuge due au fait que le système tourne autour du centre de masse du système Terre-corps céleste, qui n'est pas au centre de la Terre. Cependant, les valeurs obtenues pour le cas de la Lune sont très différentes du côté faisant face à la Lune par rapport au côté opposé de la Terre. De plus, il serait difficile d'expliquer le phénomène de cette manière si l'on considère le Soleil comme le corps céleste, car dans ce cas, le centre de masse est proche du centre du Soleil.
La manière la plus simple et qui produit des valeurs observées est de supposer qu'il s'agit d'un problème de différences de gravité et de déplacement des objets. Ainsi :
• La marée en direction du côté du corps céleste est due à son attraction, qui réduit l'accélération gravitationnelle de la Terre.
• La marée du côté opposé du corps céleste se produit à la fois en raison de la réduction de l'attraction du corps céleste et du fait que la Terre est déplacée "dans l'eau".
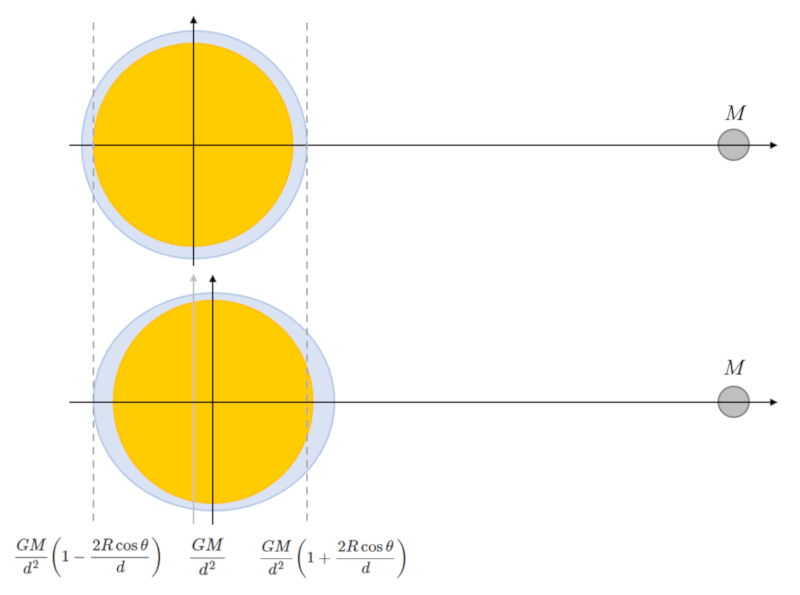
ID:(11640, 0)
Modèle
Top 
Paramètres
Variables
Calculs
Calculs
Calculs
Équations
a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }
a_o = G * M /( d ^2 + R ^2 + 2* d * R * cos( theta ))
\displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }
Da_ox / a_o = ( d + R * cos( theta ))/sqrt( d ^2 + R ^2 + 2 * d * R * cos( theta ))
\Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)
Da_ox = G * M * (1-2* R * cos( theta )/ d )/ d ^2
ID:(15435, 0)
Variation de l'accélération parallèle au rayon, en opposition
Équation 
Pour déterminer la variation de l'accélération dans le rayon, nous pouvons égaler la relation
\displaystyle\frac{\Delta a_{ox}}{a_o}
avec la longueur
d+R\cos\theta
et l'hypoténuse
\sqrt{d^2+R^2+2dR\cos\theta}
Par similitude des triangles, nous obtenons avec que:
ID:(11646, 0)
Accélération parallèle au rayon, en opposition
Équation 
Avec la loi de la gravitation de Newton, représentée par ,
| F = G \displaystyle\frac{ m_g M }{ r ^2} |
,
nous pouvons définir la force avec ,
| F = m_i a |
,
et le carré du rayon
r^2=d^2+R^2+2dR\cos\theta
,
pour calculer l'accélération avec :
ID:(11651, 0)
Accélération d'approche parallèle au rayon, en opposition
Équation 
Avec et rayon de la planète m, la relation est
| \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } } |
,
et avec et rayon de la planète m, l'expression est
| a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta } |
,
donc
\Delta a_{ox} =GM\displaystyle\frac{d + R\cos\theta}{(d^2 + R^2 + 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1-\displaystyle\frac{2R\cos\theta}{d}\right)
,
donc dans l'approximation d\gg R et en ne considérant que la variation par rapport au côté opposé, il peut être approximé avec et rayon de la planète m comme:
ID:(11649, 0)
