Utilisateur: 
Force de gravité et marées en conjonction
Storyboard 
La gravité et l'accélération centrifuge génèrent les marées, le mouvement des océans qui élève et abaisse leur niveau avec une fréquence de 12 heures. Leur origine peut être générée aussi bien par la lune que par le soleil.
ID:(1523, 0)
Variation de la gravité perpendiculaire au rayon, en conjonction
Image
Il y a une contribution de l'attraction gravitationnelle du corps céleste qui attire l'eau vers la région équatoriale :
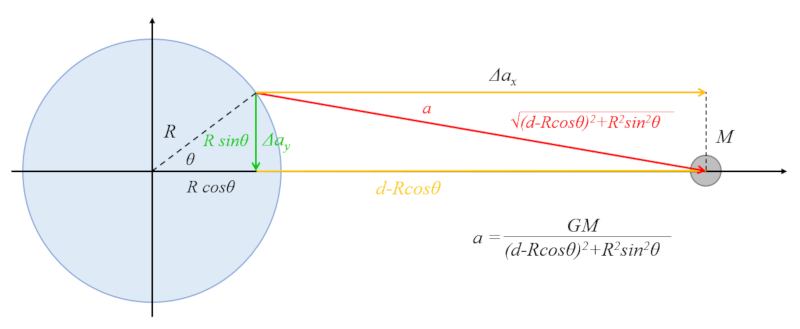
L'hypoténuse du triangle est liée au catéto vertical par :
$R\sin\theta$
et au catéto horizontal par :
$d - R\cos\theta$
Selon le théorème de Pythagore, la somme des carrés des catétos est égale au carré de l'hypoténuse, donc nous obtenons :
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11635, 0)
Variation de la gravité parallèle au rayon, en conjonction
Image
Il existe une contribution de l'attraction gravitationnelle du corps céleste qui attire l'eau vers le rayon, ce qui a tendance à déplacer l'eau vers la zone de l'équateur :
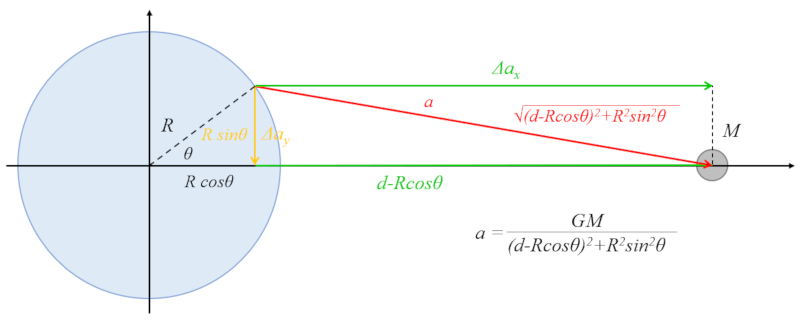
L'hypoténuse du triangle est formée par le catéte vertical :
$R\sin\theta$
et le catéte horizontal :
$d - R\cos\theta$
Selon le théorème de Pythagore, nous avons :
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11658, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$
a_c = G * M /( d ^2+ R ^2-2* d * R *cos( theta ))
$ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cx / a_c = ( d - R * cos( theta ))/sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_cx = G * M *(1 + 2* R * cos( theta )/ d )/ d ^2
$ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cy / a_c = R * sin( theta ) / sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$
Da_cy = G * M * R * sin( theta )/ d ^3
ID:(15434, 0)
Variation de l'accélération perpendiculaire au rayon, en conjonction
Équation
Pour déterminer la variation de l'accélération perpendiculaire au rayon, nous pouvons utiliser la similitude de triangles pour égaliser la relation
$\displaystyle\frac{\Delta a_{cy}}{a_c}$
avec le comprimento
$d-R\cos\theta$
et l'hypoténuse
$\sqrt{d^2+R^2-2dR\cos\theta}$
.
Par la similitude de triangles, nous avons avec que
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
.
ID:(11643, 0)
Accélération perpendiculaire au rayon, en conjonction
Équation
Avec la loi de la gravitation de Newton, avec , c'est:
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
On peut, avec la définition de la force, avec :
| $ F = m_i a $ |
Et le rayon au carré:
$r^2=d^2+R^2-2dR\cos\theta$
Calculer l'accélération en remplaçant le rayon dans la force et en résolvant l'accélération. Cela donne avec l'accélération:
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
ID:(11644, 0)
Accélération d'approche perpendiculaire au rayon, en conjonction
Équation
Avec , la relation entre la variation de l'accélération et l'accélération est :
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
Et comme l'expression pour l'accélération est avec :
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
Il en résulte que :
$\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}$
Par conséquent, dans l'approximation
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
ID:(11645, 0)
Variation de l'accélération parallèle au rayon, en conjonction
Équation
Pour déterminer la variation de l'accélération parallèle au rayon, nous pouvons utiliser la similitude des triangles pour égaliser la relation
$\displaystyle\frac{\Delta a_{cx}}{a_c}$
avec la longueur
$d+R\cos\theta$
et l'hypoténuse
$\sqrt{d^2+R^2-2dR\cos\theta}$
Par similitude de triangles, nous avons avec que
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
ID:(11647, 0)
Accélération d'approche parallèle au rayon, en conjonction
Équation
Avec et rayon de la planète $m$, la relation est :
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
Et comme pour et rayon de la planète $m$,
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
Ainsi, nous avons :
$\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)$
Par conséquent, dans l'approximation
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11650, 0)