Druyd:Knowledge

Schwerkraft und Gezeiten in Konjunktion

Storyboard

Gravitation und Zentrifugalbeschleunigung erzeugen Gezeiten, die Bewegung der Ozeane, die ihren Pegel alle 12 Stunden anheben und senken. Ihre Ursache kann sowohl der Mond als auch die Sonne sein.

>Modell

ID:(1523, 0)

Mechanismen

Iframe

>Top

Wissen

Code

Konzept

Mechanismen

ID:(15439, 0)

Variation der Schwerkraft senkrecht zum Radius in Verbindung

Bild

>Top

Es gibt einen Beitrag von der Gravitationsattraktion des Himmelskörpers, der Wasser zum Äquator hin zieht:

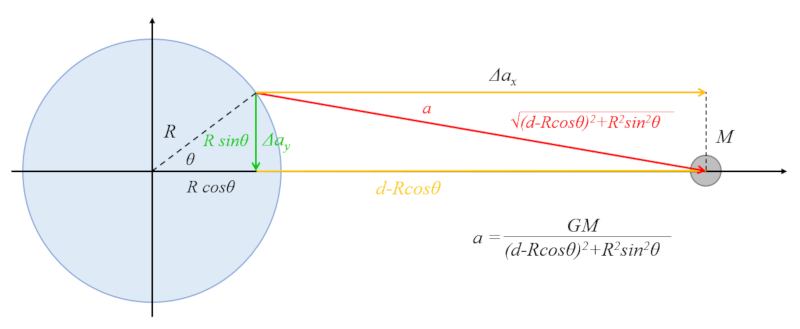
Die Hypotenuse des Dreiecks ist mit dem senkrechten Kathetens durch die Gleichung verbunden:

$R\sin\theta$

und mit dem horizontalen Katheten durch:

$d - R\cos\theta$

Nach dem Satz des Pythagoras ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse, daher ergibt sich:

$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$

ID:(11635, 0)

Variation der Schwerkraft parallel zum Radius in Verbindung

Bild

>Top

Es gibt einen Beitrag von der Gravitationsattraktion des Himmelskörpers, der das Wasser zum Radius hin zieht, was dazu neigt, das Wasser in Richtung des Äquators zu verschieben:

Die Hypotenuse des Dreiecks wird durch das senkrechte Bein gebildet:

$R\sin\theta$

und das horizontale Bein:

$d - R\cos\theta$

Gemäß dem Satz des Pythagoras haben wir:

$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$

ID:(11658, 0)

Modell

Top

>Top

Parameter

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$\Delta a_{cx}$

Da_cx

Beschleunigungsvariation parallel zur Ekliptik, in Konjunktion

m/s^2

$\Delta a_{cy}$

Da_cy

Beschleunigungsvariation perpendicular zur Ekliptik

m/s^2

$d$

Entfernung des Himmelsobjektplaneten

$M$

Masa del cuerpo que genera la marea

$R$

Planetenradio

$G$

Universelle Gravitationskonstante

m^3/kg s^2

$a_c$

a_c

Vom Himmelskörper erzeugte Beschleunigung, in Konjunktion

m/s^2

$\theta$

theta

Winkel von der Planetenlinie - Himmelsobjekt

rad

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

Gleichung

$a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$

a_c = G * M /( d ^2+ R ^2-2* d * R *cos( theta ))

$\displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$

Da_cx / a_c = ( d - R * cos( theta ))/sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))

$\Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$

Da_cx = G * M *(1 + 2* R * cos( theta )/ d )/ d ^2

$\displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$

Da_cy / a_c = R * sin( theta ) / sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))

$\Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$

Da_cy = G * M * R * sin( theta )/ d ^3

ID:(15434, 0)

Variation der Beschleunigung senkrecht zum Radius in Verbindung

Gleichung

>Top, >Modell

Um die Variation der Beschleunigung senkrecht zum Radius zu bestimmen, können wir die Ähnlichkeit von Dreiecken verwenden, um die Beziehung

$\displaystyle\frac{\Delta a_{cy}}{a_c}$

mit der Länge

$d-R\cos\theta$

und der Hypotenuse

$\sqrt{d^2+R^2-2dR\cos\theta}$

auszugleichen.

Durch die Ähnlichkeit von Dreiecken ergibt sich mit , dass

$\displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$

$\Delta a_{cy}$

Beschleunigungsvariation perpendicular zur Ekliptik

$m/s^2$

8576

$d$

Entfernung des Himmelsobjektplaneten

$m$

8567

$R$

Planetenradio

$m$

8566

$a_c$

Vom Himmelskörper erzeugte Beschleunigung, in Konjunktion

$m/s^2$

8572

$\theta$

Winkel von der Planetenlinie - Himmelsobjekt

$rad$

8569

ID:(11643, 0)

Beschleunigung senkrecht zum radius in Verbindung

Gleichung

>Top, >Modell

Mit dem Gravitationsgesetz von Newton, mit , ist:

$F = G \displaystyle\frac{ m_g M }{ r ^2}$

Es ist möglich, mit der Definition der Kraft, mit :

$F = m_i a$

Und dem Radius zum Quadrat:

$r^2=d^2+R^2-2dR\cos\theta$

Die Beschleunigung zu berechnen, indem man den Radius in die Kraft einsetzt und die Beschleunigung ausdrückt. Das ergibt mit die Beschleunigung:

$a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$

$d$

Entfernung des Himmelsobjektplaneten

$m$

8567

$M$

Masa del cuerpo que genera la marea

$kg$

8568

$R$

Planetenradio

$m$

8566

$G$

Universelle Gravitationskonstante

$m^3/kg s^2$

8564

$a_c$

Vom Himmelskörper erzeugte Beschleunigung, in Konjunktion

$m/s^2$

8572

$\theta$

Winkel von der Planetenlinie - Himmelsobjekt

$rad$

8569

ID:(11644, 0)

Beschleunigungsnäherung senkrecht zum Radius in Verbindung

Gleichung

>Top, >Modell

Mit beschleunigungsvariation perpendicular zur Ekliptik $m/s^2$ , entfernung des Himmelsobjektplaneten $m$ , planetenradio $m$ , vom Himmelskörper erzeugte Beschleunigung, in Konjunktion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ ist die Beziehung zwischen der Variation der Beschleunigung und der Beschleunigung:

$\displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$

Und da der Ausdruck für die Beschleunigung mit entfernung des Himmelsobjektplaneten $m$ , masa del cuerpo que genera la marea $kg$ , planetenradio $m$ , universelle Gravitationskonstante $m^3/kg s^2$ , vom Himmelskörper erzeugte Beschleunigung, in Konjunktion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ ist:

$a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$

Folgt:

$\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}$

Daher können wir in der Näherung d\gg R mit approximieren:

$\Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$

$\Delta a_{cy}$

Beschleunigungsvariation perpendicular zur Ekliptik

$m/s^2$

8576

$d$

Entfernung des Himmelsobjektplaneten

$m$

8567

$M$

Masa del cuerpo que genera la marea

$kg$

8568

$R$

Planetenradio

$m$

8566

$G$

Universelle Gravitationskonstante

$m^3/kg s^2$

8564

$\theta$

Winkel von der Planetenlinie - Himmelsobjekt

$rad$

8569

ID:(11645, 0)

Beschleunigungsvariation parallel zum Radius, in Konjunktion

Gleichung

>Top, >Modell

Um die Variation der Beschleunigung parallel zum Radius zu bestimmen, können wir die Ähnlichkeit von Dreiecken verwenden, um die Beziehung

$\displaystyle\frac{\Delta a_{cx}}{a_c}$

mit der Länge

$d+R\cos\theta$

und der Hypotenuse

$\sqrt{d^2+R^2-2dR\cos\theta}$

auszugleichen.

Durch die Ähnlichkeit von Dreiecken ergibt sich mit , dass

$\displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$

$\Delta a_{cx}$

Beschleunigungsvariation parallel zur Ekliptik, in Konjunktion

$m/s^2$

8575

$d$

Entfernung des Himmelsobjektplaneten

$m$

8567

$R$

Planetenradio

$m$

8566

$a_c$

Vom Himmelskörper erzeugte Beschleunigung, in Konjunktion

$m/s^2$

8572

$\theta$

Winkel von der Planetenlinie - Himmelsobjekt

$rad$

8569

ID:(11647, 0)

Annäherungsbeschleunigung parallel zum Radius, in Konjunktion

Gleichung

>Top, >Modell

Mit beschleunigungsvariation parallel zur Ekliptik, in Konjunktion $m/s^2$ , entfernung des Himmelsobjektplaneten $m$ , planetenradio $m$ , vom Himmelskörper erzeugte Beschleunigung, in Konjunktion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ ist die Beziehung:

$\displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$

Und wie für entfernung des Himmelsobjektplaneten $m$ , masa del cuerpo que genera la marea $kg$ , planetenradio $m$ , universelle Gravitationskonstante $m^3/kg s^2$ , vom Himmelskörper erzeugte Beschleunigung, in Konjunktion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ ,

$a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$

Somit haben wir:

$\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)$

Daher können wir in der Näherung d\gg R mit approximieren:

$\Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$

$\Delta a_{cx}$

Beschleunigungsvariation parallel zur Ekliptik, in Konjunktion

$m/s^2$

8575

$d$

Entfernung des Himmelsobjektplaneten

$m$

8567

$M$

Masa del cuerpo que genera la marea

$kg$

8568

$R$

Planetenradio

$m$

8566

$G$

Universelle Gravitationskonstante

$m^3/kg s^2$

8564

$\theta$

Winkel von der Planetenlinie - Himmelsobjekt

$rad$

8569

ID:(11650, 0)