User: 
Force of gravity and tides in conjunction
Storyboard 
Gravity and centrifugal acceleration generate tides, the movement of oceans that raises and lowers their level with a frequency of 12 hours. Their origin can be generated by both the moon and the sun.
ID:(1523, 0)
Variation of gravity perpendicular to the radius, in conjunction
Image
There is a contribution from the gravitational attraction of the celestial body that pulls water towards the equatorial region:
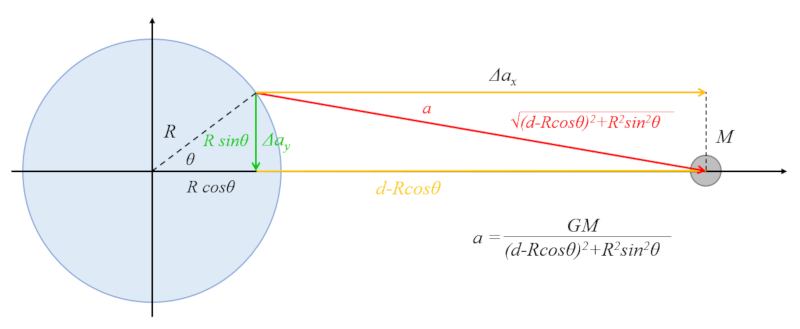
The hypotenuse of the triangle is related to the vertical leg by:
R\sin\theta
and the horizontal leg by:
d - R\cos\theta
Using the Pythagorean theorem, we have:
R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta
ID:(11635, 0)
Variation of gravity parallel to the radius, in conjunction
Image
There is a contribution from the gravitational attraction of the celestial body that pulls water towards the radius, which tends to displace the water towards the equatorial zone:
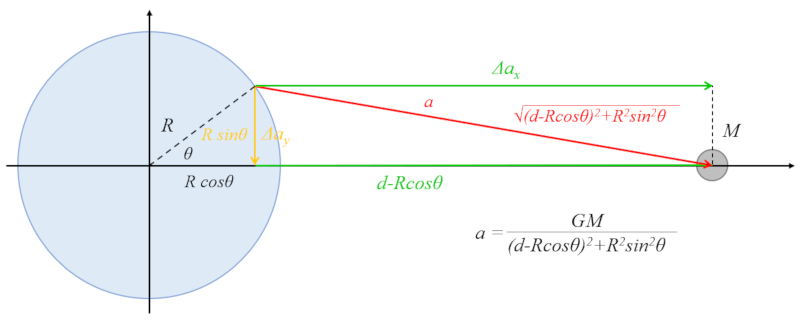
The hypotenuse of the triangle is formed by the vertical leg:
R\sin\theta
and the horizontal leg:
d - R\cos\theta
According to the Pythagorean theorem, we have:
R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta
ID:(11658, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }
a_c = G * M /( d ^2+ R ^2-2* d * R *cos( theta ))
\displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }
Da_cx / a_c = ( d - R * cos( theta ))/sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
\Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)
Da_cx = G * M *(1 + 2* R * cos( theta )/ d )/ d ^2
\displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }
Da_cy / a_c = R * sin( theta ) / sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
\Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }
Da_cy = G * M * R * sin( theta )/ d ^3
ID:(15434, 0)
Variation of acceleration perpendicular to the radius, in conjunction
Equation
To determine the variation of the acceleration perpendicular to the radius, we can use triangle similarity to equate the relation
\displaystyle\frac{\Delta a_{cy}}{a_c}
with the length
d-R\cos\theta
and the hypotenuse
\sqrt{d^2+R^2-2dR\cos\theta}
.
By triangle similarity, we have with that
| \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } } |
.
ID:(11643, 0)
Acceleration perpendicular to the radius, in conjunction
Equation
Con la ley de la gravitación de Newton, con , es:
| F = G \displaystyle\frac{ m_g M }{ r ^2} |
Se puede, con la definición de la fuerza, con :
| F = m_i a |
Y el radio al cuadrado:
r^2=d^2+R^2-2dR\cos\theta
Calcular la aceleración reemplazando el radio en la fuerza y despejando la aceleración. Esto da con la aceleración:
| a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta } |
ID:(11644, 0)
Acceleration approximation perpendicular to the radius, in conjunction
Equation
With acceleration generated by the celestial body, en conjunction m/s^2, acceleration variation perpendicular to the ecliptic m/s^2, angle from the planet line - celestial object rad, celestial object planet distance m and planet radio m, the relationship between the variation of acceleration and acceleration is:
| \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } } |
And since the expression for acceleration is with acceleration generated by the celestial body, en conjunction m/s^2, angle from the planet line - celestial object rad, celestial object planet distance m, masa del cuerpo que genera la marea kg, planet radio m and universal Gravitation Constant m^3/kg s^2:
| a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta } |
It follows that:
\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}
Therefore, in the approximation
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
ID:(11645, 0)
Acceleration variation parallel to the radius, in conjunction
Equation
To determine the variation of the acceleration parallel to the radius, we can use triangle similarity to equate the relation
\displaystyle\frac{\Delta a_{cx}}{a_c}
with the length
d+R\cos\theta
and the hypotenuse
\sqrt{d^2+R^2-2dR\cos\theta}
By triangle similarity, we have with that
| \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } } |
ID:(11647, 0)
Approach acceleration parallel to the radius, in conjunction
Equation
With acceleration generated by the celestial body, en conjunction m/s^2, acceleration variation parallel to the ecliptic, in conyunction m/s^2, angle from the planet line - celestial object rad, celestial object planet distance m and planet radio m, the relationship is:
| \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } } |
And as for acceleration generated by the celestial body, en conjunction m/s^2, angle from the planet line - celestial object rad, celestial object planet distance m, masa del cuerpo que genera la marea kg, planet radio m and universal Gravitation Constant m^3/kg s^2,
| a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta } |
Thus, we have:
\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)
Therefore, in the approximation
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
ID:(11650, 0)