Force of gravity and tides in opposition
Storyboard 
One of the accelerations that needs to be calculated is the one parallel to the ecliptic (in the Earth-celestial body plane) in opposition, meaning on the opposite side of the celestial body.
ID:(1575, 0)
Variation of gravity parallel to the radius, as opposed to
Image 
The attraction on the opposite side of the celestial body acting on Earth is weaker due to the greater distance. This facilitates water displacement towards the equator. On the side facing the celestial body, its gravitational attraction weakens Earth's gravitational acceleration, leading to a reduction in gravity that further aids water displacement towards the equator:
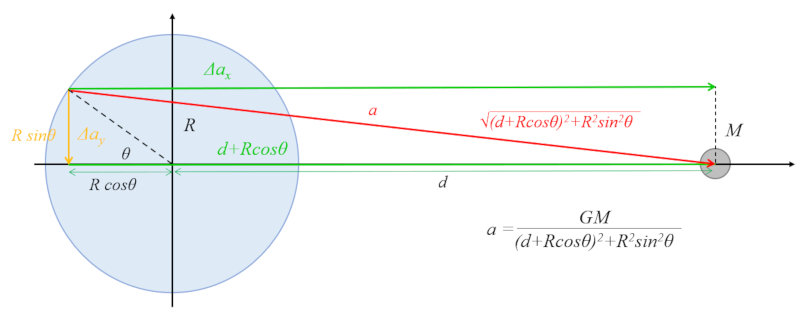
In this case, we work with similarity in the triangle, where we take the proportion
\Delta a_{ox}/a_o
and the leg
d + R\cos\theta
and the hypotenuse
(d+R\cos\theta)^2+R^2\sin^2\theta=d^2+R^2+2dR\cos\theta
ID:(11639, 0)
Intuitive explanation of the tide on the side opposite the celestial body
Image 
There are multiple explanations for the tides on the opposite side of the celestial body. One of them is the effect of centrifugal acceleration due to the fact that the system rotates around the center of mass of the Earth-celestial body system, which is not at the center of the Earth. However, the values obtained for the case of the moon are very different on the side facing the moon compared to the opposite side of the Earth. Additionally, it would be difficult to explain the phenomenon in this way if the sun is taken as the celestial body since in that case the center of mass is near the center of the sun.
The simplest explanation that yields values like those observed is to assume that it is a problem of gravity differences and displacement of objects. Therefore:
• The tide toward the side of the celestial body originates from its attraction, which reduces the gravitational acceleration of the Earth.
• The tide on the opposite side of the celestial body occurs both due to the reduction of the celestial body's attraction and also because the Earth is displaced "within the water."
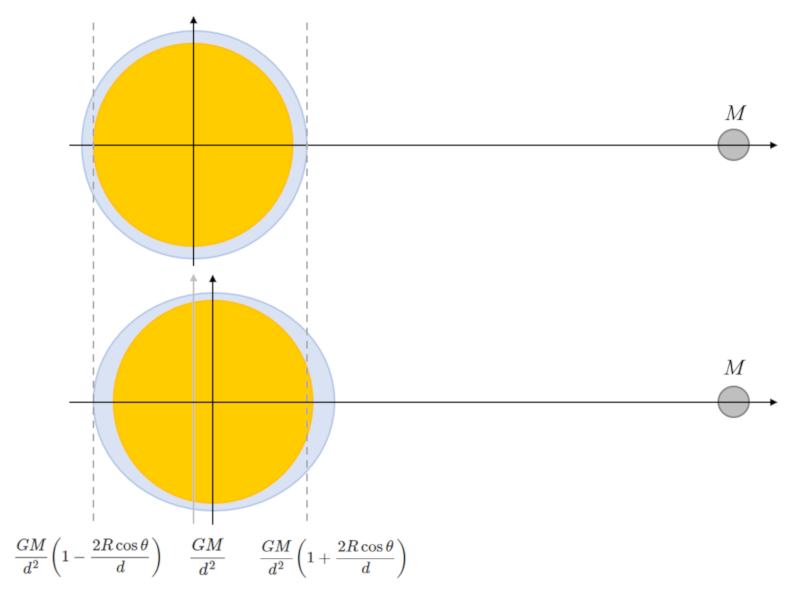
ID:(11640, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }
a_o = G * M /( d ^2 + R ^2 + 2* d * R * cos( theta ))
\displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }
Da_ox / a_o = ( d + R * cos( theta ))/sqrt( d ^2 + R ^2 + 2 * d * R * cos( theta ))
\Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)
Da_ox = G * M * (1-2* R * cos( theta )/ d )/ d ^2
ID:(15435, 0)
Variation of acceleration parallel to the radius, as opposed to
Equation 
To determine the variation of acceleration along the radius, we can equate the relationship
\displaystyle\frac{\Delta a_{ox}}{a_o}
with the length
d+R\cos\theta
and the hypotenuse
\sqrt{d^2+R^2+2dR\cos\theta}
By similarity of triangles, we obtain with that:
ID:(11646, 0)
Acceleration parallel to the radius, as opposed to
Equation 
With Newton's law of gravitation, represented by ,
| F = G \displaystyle\frac{ m_g M }{ r ^2} |
,
we can define the force with ,
| F = m_i a |
,
and the squared radius
r^2=d^2+R^2+2dR\cos\theta
,
to calculate the acceleration with :
ID:(11651, 0)
Approximation acceleration parallel to the radius, as opposed to
Equation 
With acceleration generated by the celestial body, en oposition m/s^2, acceleration variation parallel to the ecliptic, in oposition m/s^2, angle from the planet line - celestial object rad, celestial object planet distance m and planet radio m, the relationship is
| \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } } |
,
and with acceleration generated by the celestial body, en oposition m/s^2, angle from the planet line - celestial object rad, celestial object planet distance m, masa del cuerpo que genera la marea kg, planet radio m and universal Gravitation Constant m^3/kg s^2, the expression is
| a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta } |
,
thus
\Delta a_{ox} =GM\displaystyle\frac{d + R\cos\theta}{(d^2 + R^2 + 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1-\displaystyle\frac{2R\cos\theta}{d}\right)
,
so in the approximation
ID:(11649, 0)
