Druyd:Knowledge

Solar and lunar tides

Storyboard

The second type of tides that are recorded on land are solar tides. Its size is less than that of the moon.

>Model

ID:(1576, 0)

Mechanisms

Iframe

>Top

Knowledge

Code

Concept

Mechanisms

ID:(15441, 0)

Parallel increase in acceleration generated, as opposed to

Image

>Top

The change in gravitational acceleration leads to a flow of water that tends to alter the height of the water column (sea depth) in order to compensate for pressure:

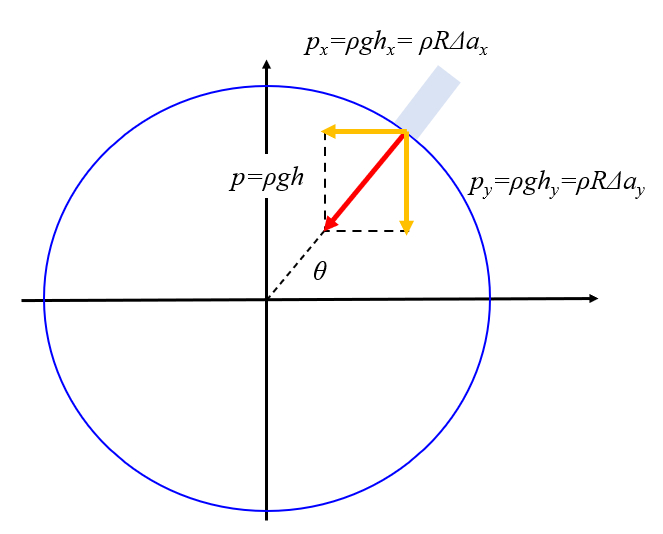
ID:(11652, 0)

Representation as ellipse

Image

>Top

Variations in acceleration lead to changes in water pressure around the planet, allowing water columns to differ in heights.

In particular, the deviations caused are as follows:

For the sun's case: 8.14 cm, 16.28 cm
For the moon's case: 17.9 cm, 35.6 cm

This situation can be represented as a deformation of a circle, corresponding to an ellipse.

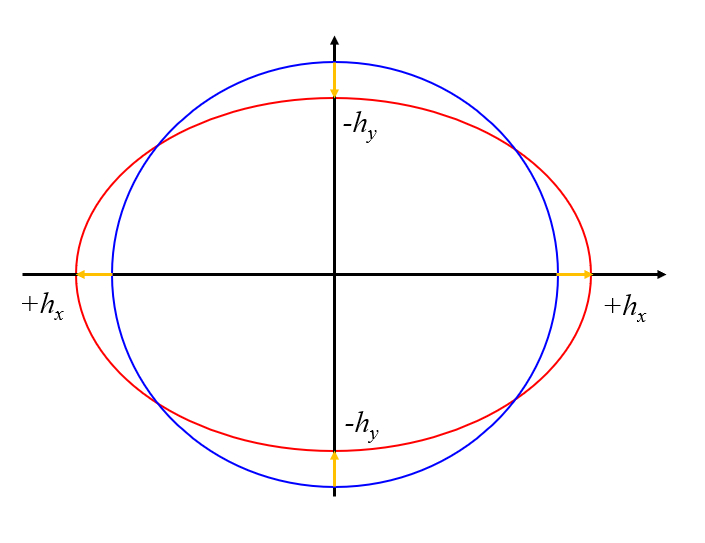
ID:(11657, 0)

Sun case parameters

Image

>Top

In the case of the sun,

the following parameters are considered:

Mass: 1.987e+30 kg
Sun-Earth distance: 1.50e+11 m

The tidal heights can be calculated using the following relationships:

For the x-direction, with angle from the planet line - celestial object $rad$ , celestial object planet distance $m$ , gravitational Acceleration $m/s^2$ , masa del cuerpo que genera la marea $kg$ , planet radio $m$ , tidal height parallel to the ecliptic $m$ and universal Gravitation Constant $m^3/kg s^2$ , we have:

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta$

And for the y-direction, with angle from the planet line - celestial object $rad$ , celestial object planet distance $m$ , gravitational Acceleration $m/s^2$ , masa del cuerpo que genera la marea $kg$ , planet radio $m$ , tidal height perpendicular to the ecliptic $m$ and universal Gravitation Constant $m^3/kg s^2$ , we obtain:

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

With the Earth's radius of 6371 km, at the point of minimum tide ( $\theta = \pi/2$ ), we have:

$h_y = 8.14 cm$

And at the point of maximum tide ( $\theta = 0$ ), it is:

$h_x = 16.28 cm$

Thus, the fluctuations due to the sun amount to $h_x + h_y = 24.42 cm$ .

ID:(11656, 0)

Moon case parameters

Image

>Top

In the case of the Moon,

we have the following parameters:

Mass: 7.349e+22 kg
Distance Earth-Moon: 3.84e+8 m

For the x-direction, with angle from the planet line - celestial object $rad$ , celestial object planet distance $m$ , gravitational Acceleration $m/s^2$ , masa del cuerpo que genera la marea $kg$ , planet radio $m$ , tidal height parallel to the ecliptic $m$ and universal Gravitation Constant $m^3/kg s^2$ , we have:

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta$

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

With the Earth's radius of 6371 km, at the point of lowest tide ( $\theta = \pi/2$ ), we obtain:

$h_y = 17.9 cm$

And at the point of highest tide ( $\theta = 0$ ), we have:

$h_x = 35.6 cm$

So, the fluctuations due to the Moon amount to $h_x + h_y = 53.5 cm$ .

ID:(11655, 0)

Model

Top

>Top

Parameters

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$\Delta a_{cx}$

Da_cx

Acceleration variation parallel to the ecliptic, in conyunction

m/s^2

$\Delta a_{ox}$

Da_ox

Acceleration variation parallel to the ecliptic, in oposition

m/s^2

$\Delta a_{cy}$

Da_cy

Acceleration variation perpendicular to the ecliptic

m/s^2

$\theta$

theta

Angle from the planet line - celestial object

rad

$d$

Celestial object planet distance

$g$

Gravitational Acceleration

m/s^2

$M$

Masa del cuerpo que genera la marea

$R$

Planet radio

$h_x$

h_x

Tidal height parallel to the ecliptic

$h_y$

h_y

Tidal height perpendicular to the ecliptic

$G$

Universal Gravitation Constant

m^3/kg s^2

Variables

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

Calculations

Equation

Number

First, select the equation:

, then, select the variable:

Calculations

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable

Given

Calculate

Target :

Equation

To be used

Equations

Equation

$g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R$

g * h_x = ( Da_cx - Da_ox )* R / 2

$g h_y = \Delta a_{cy} R$

g * h_y = Da_cy * R

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta$

h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

h_y = G * M * R ^2* sin( theta )/( g * d ^3)

ID:(15437, 0)

Depth relationship and acceleration variation in x

Equation

>Top, >Model

The change in acceleration means that the water column experiences a different pressure unless the depth adjusts. To achieve a steady state, this is precisely what happens. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

$p_x=\rho g h_x=\rho\displaystyle\frac{1}{2} (\Delta a_{cx} - \Delta a_{ox}) R$

Therefore,

$g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R$

$\Delta a_{cx}$

Acceleration variation parallel to the ecliptic, in conyunction

$m/s^2$

8575

$\Delta a_{ox}$

Acceleration variation parallel to the ecliptic, in oposition

$m/s^2$

8574

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$R$

Planet radio

$m$

8566

$h_x$

Tidal height parallel to the ecliptic

$m$

8570

ID:(13215, 0)

Depth variation in the x direction

Equation

>Top, >Model

The change in acceleration implies that the column of water experiences a different pressure unless the depth adjusts. Achieving a steady state involves precisely this. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

$g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R$

With the variation on the conjunction side with

$\Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$

and with

$\Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$

It follows that the surface rises with in

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta$

$\theta$

Angle from the planet line - celestial object

$rad$

8569

$d$

Celestial object planet distance

$m$

8567

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$M$

Masa del cuerpo que genera la marea

$kg$

8568

$R$

Planet radio

$m$

8566

$h_x$

Tidal height parallel to the ecliptic

$m$

8570

$G$

Universal Gravitation Constant

$m^3/kg s^2$

8564

where only the variable part of the variation was taken into account, since the term $GM/d^2$ acts on the entire system and does not create differences.

ID:(11653, 0)

Depth relationship and acceleration variation in y

Equation

>Top, >Model

$p_y=\rho g h_y=\rho\Delta a_{cy} R$

Therefore, it follows that:

$g h_y = \Delta a_{cy} R$

$\Delta a_{cy}$

Acceleration variation perpendicular to the ecliptic

$m/s^2$

8576

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$R$

Planet radio

$m$

8566

$h_y$

Tidal height perpendicular to the ecliptic

$m$

8571

ID:(13216, 0)

Depth variation in the y direction

Equation

>Top, >Model

The change in acceleration means that the column of water experiences a different pressure unless the depth adjusts. To achieve a steady state, this is precisely what happens. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

$g h_y = \Delta a_{cy} R$

With the variation on the side of conjunction with

$\Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$

As a result, the surface rises with at

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

$\theta$

Angle from the planet line - celestial object

$rad$

8569

$d$

Celestial object planet distance

$m$

8567

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$M$

Masa del cuerpo que genera la marea

$kg$

8568

$R$

Planet radio

$m$

8566

$h_y$

Tidal height perpendicular to the ecliptic

$m$

8571

$G$

Universal Gravitation Constant

$m^3/kg s^2$

8564

ID:(11654, 0)