Utilizador:
Velocidade do som no mar
Storyboard 
A velocidade do som no mar depende da pressão, temperatura e salinidade.
ID:(1548, 0)
Velocidade do som com profundidade
Conceito
A velocidade do som no oceano varia com a profundidade, conforme mostrado no gráfico:
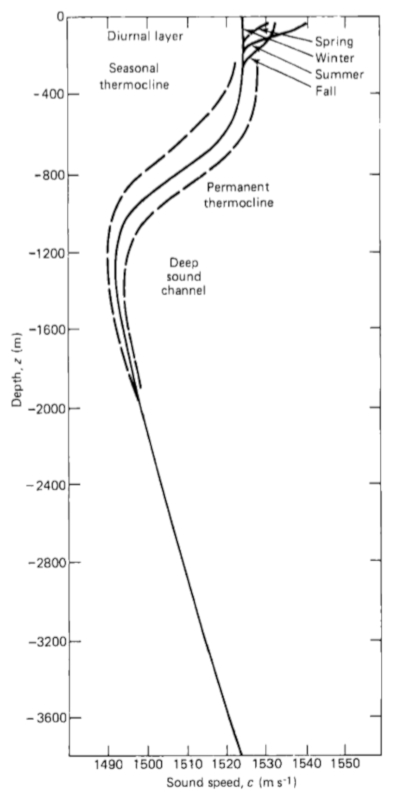
A forma da curva pode variar dependendo da época do ano.
ID:(11814, 0)
Dependência da velocidade do som
Conceito
A velocidade do som no oceano depende da temperatura e da pressão, conforme mostrado no gráfico:
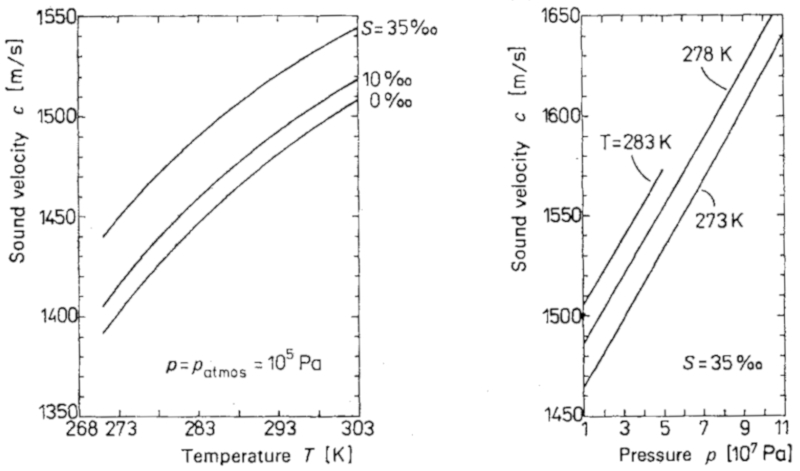
ID:(11815, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ c = c_0 T ^3- c_1 T ^2+( c_3 - c_2 s ) T + c_4 p + c_5 s - c_6 $
c = c_0 * T ^3- c_1 * T ^2+( c_3 - c_2 * s )* T + c_4 * p +c_5 * s - c_6
$\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$
sin( theta_i )/sin( theta_r )= c_i / c_e
ID:(15465, 0)
Equação da velocidade do som
Equação
Em 1977, Clay e Medwin desenvolveram um modelo para estimar a velocidade do som em função da temperatura, salinidade e pressão.
A velocidade do som la velocidade do som ($c$)8652 pode ser estimada com base em ($$)8800, la temperatura ($T$)8791 e la salinidade ($s$)8792 usando a seguinte expressão:
| $ c = c_0 T ^3- c_1 T ^2+( c_3 - c_2 s ) T + c_4 p + c_5 s - c_6 $ |
onde $c_i$ são constantes empíricas.
Referência: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah e Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, novembro de 2017.
ID:(11816, 0)