Druyd:Knowledge

Loading web-font TeX/Math/Italic

Absorption, dispersion and sound sources

Storyboard

The attenuation of sound waves in the ocean depends on the frequency of the sound. For low frequencies (below 10 kHz), the main contribution comes from boric acid ions, while in the range between 10 kHz and 100 kHz, it is due to the effect of magnesium sulfate ions. For higher frequencies, attenuation is primarily due to the viscosity of the water.

ID:(1549, 0)

Mechanisms

Iframe

Code

Concept

Mechanisms

ID:(15464, 0)

Bottom disturbance

Image

Slopes in the background lead to disturbances in sound propagation:

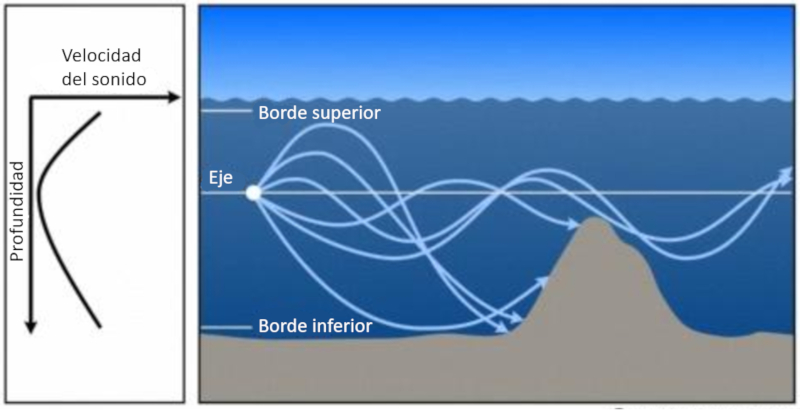
ID:(11824, 0)

Sound generation

Image

There are different sources of sound in the oceans. Among them are

• human sources (first of all ships)
• rain on the surface
• fish, shrimp, whales, etc.
• waves
• tremors

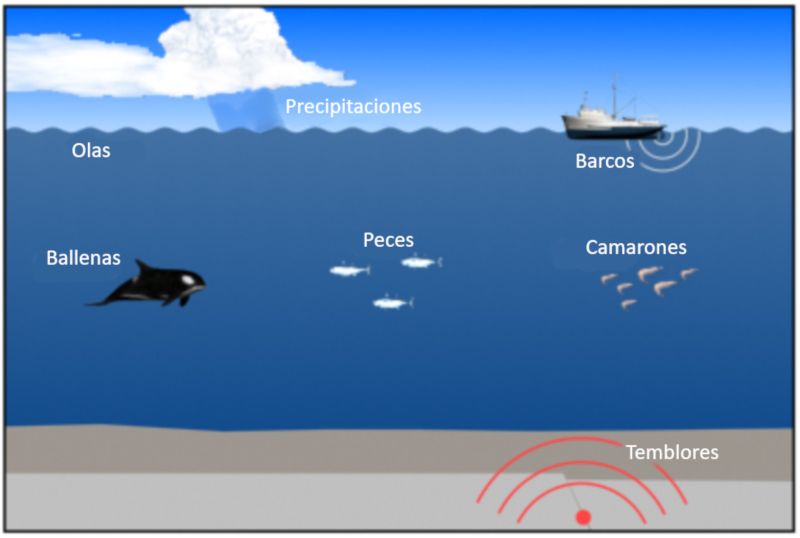
ID:(11825, 0)

Sound and its frequency

Image

The spectra of the sources, which correspond to the measurement of the amplitudes of the sound according to their frequency, show the strong presence of the rains:

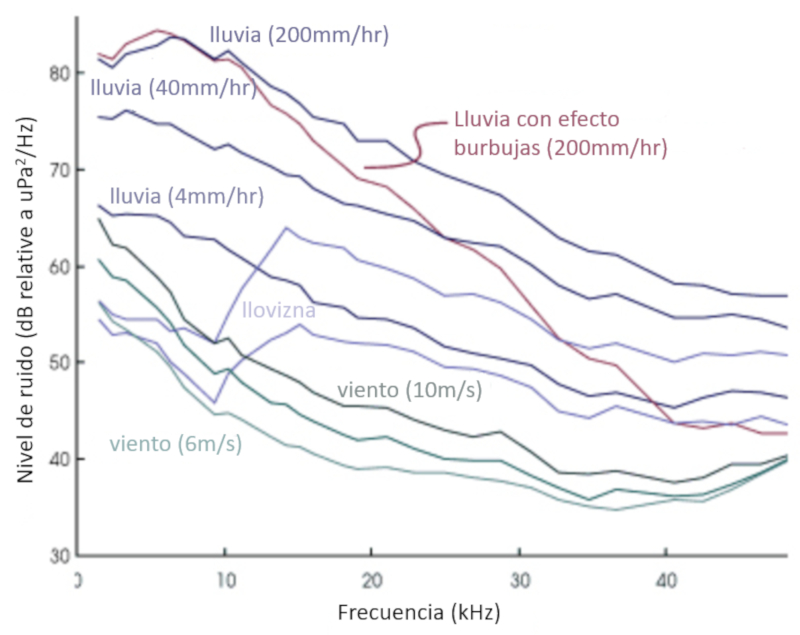
ID:(11827, 0)

Reverberation

Image

The sound emitted can generate that some elements in turn begin to generate sound. Two relevant examples in the case of the oceans are:

- air bubbles generated by waves when bursting
- methane bubbles generated when organic matter decomposes
- fish bladders:

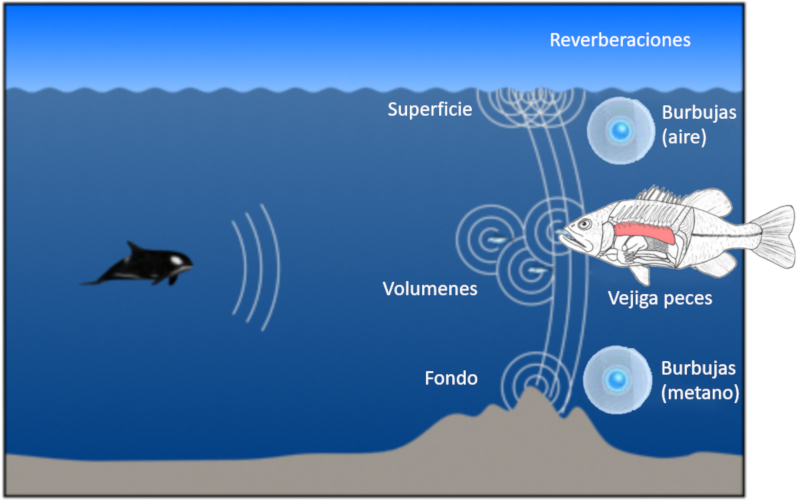
ID:(11828, 0)

Sound attenuation

Image

There are three mechanisms that attenuate sound in the sea:

• magnesium sulfate ion relaxations (up to 10kHz)
• Boric acid ion relaxations (up to 100kHz)
• water viscosity (at all frequencies)

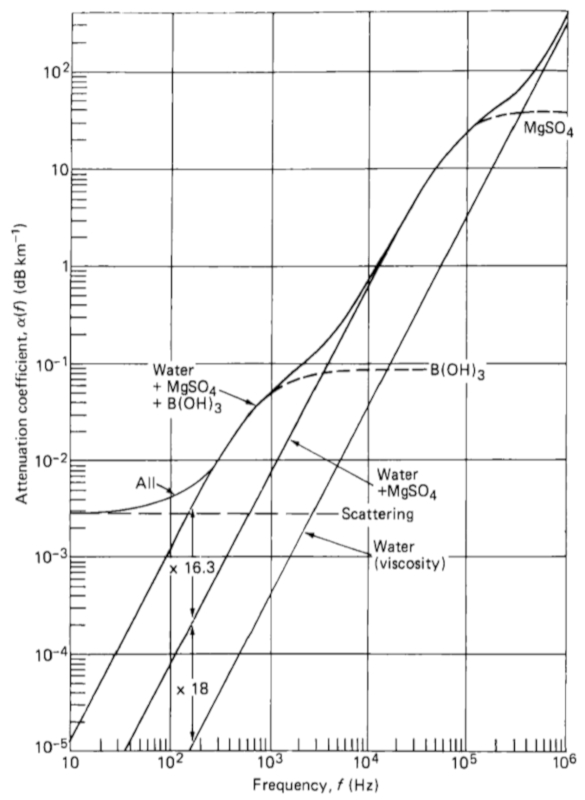
ID:(11823, 0)

Model

Top

Parameters

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$\alpha$

alpha

Absorption coefficient

1/m

$\alpha_0$

alpha_0

Absorption constants 0

1/m

$\alpha_1$

alpha_1

Constantes de absorción 1

1/m

$\alpha_2$

alpha_2

Constantes de absorción 2

1/m

$\alpha_3$

alpha_3

Constantes de absorción 3

1/m

Variables

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$r$

r

Emitter - reflector distance

m

$\nu$

nu

Frequency

Hz

$\nu_1$

nu_1

Frequency constant 1

Hz

$\nu_2$

nu_2

Frequency constant 2

Hz

$I_0$

I_0

Sound intensity, no absorption

W/m^2

$I$

I

Sound intensity, with absorption

W/m^2

Calculations

Equation

Number

First, select the equation:

to

, then, select the variable:

to

Calculations

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable

Given

Calculate

Target :

Equation

To be used

Equations

#

Equation

$\alpha = \alpha_1 \displaystyle\frac{ \nu ^2}{ \nu ^2+\nu_1^2} + \alpha_2 \displaystyle\frac{ \nu ^2}{ \nu ^2+ \nu_2 ^2} + \alpha_2 \nu ^2 + \alpha_0$

alpha = alpha_1 * nu ^2/( nu ^2+ nu_1 ^2) + alpha_2 * nu ^2/( nu ^2+ nu_2 ^2) + alpha_2 * nu ^2 + alpha_0

$I = I_0 e^{ - \alpha r }$

I = I_0 * exp(- alpha * r )

ID:(15467, 0)

Sound absorption effect

Equation

El factor de absorción indica como la energía se va perdido a lo largo del camino recorrido. Como la perdida es siempre proporcional a la intensidad existente se tiene un decaimiento exponencial.

Por ello con

$I = I_0 e^{ - \alpha r }$

ID:(11834, 0)

Relaxation processes in seawater

Equation

Existe una amortiguación del sonido en agua de mar por efecto de interacción de moléculas con los iones de hidróxido (OH-) o con moléculas de agua. Esto se denomina procesos de relajación y ocurren en el agua de mar principalmente con:

• moléculas de agua entre estas
• ácido bórico que interactua con los iones de hidróxido $OH^-$ s: $B(OH)_3\cdot OH^- \rightleftharpoons B(OH)_4$
• sulfato de magnesio que interactua con moléculas de agua $H_2O$ : $MgSO_4 + 2nH_2O \rightleftharpoons Mg^{2+}nH_2O + SO_4^{-2}nH_2O$

Los tiempos de relajamiento y sus frecuencias son del orden de

Componente	Tiempo de relajamiento	Frecuencia
Agua	$10^{-11}s$	$10^5,MHz$
Ácido bórico	$10^{-3}s$	$1,kHz$
Sulfato de magnesio (1)	$10^{-5}s$	$100,kHz$
Sulfato de magnesio (2)	$2\times 10^{-8}s$	$200,kHz$

Sobre esta base se estima el factor de absorción en función de la frecuencia y suponiendo pH típico:

$\alpha = \alpha_1 \displaystyle\frac{ \nu ^2}{ \nu ^2+\nu_1^2} + \alpha_2 \displaystyle\frac{ \nu ^2}{ \nu ^2+ \nu_2 ^2} + \alpha_2 \nu ^2 + \alpha_0$

Existe una amortiguación del sonido en agua de mar por efecto de interacción de moléculas con los iones de hidróxido (OH-) o con moléculas de agua. Esto se denomina procesos de relajación y ocurren en el agua de mar principalmente con:

• moléculas de agua entre estas
• ácido bórico que interactua con los iones de hidróxido $OH^-$ s: $B(OH)_3\cdot OH^- \rightleftharpoons B(OH)_4$
• sulfato de magnesio que interactua con moléculas de agua $H_2O$ : $MgSO_4 + 2nH_2O \rightleftharpoons Mg^{2+}nH_2O + SO_4^{-2}nH_2O$

Los tiempos de relajamiento y sus frecuencias son del orden de

Componente	Tiempo de relajamiento	Frecuencia
Agua	$10^{-11}s$	$10^5,MHz$
Ácido bórico	$10^{-3}s$	$1,kHz$
Sulfato de magnesio (1)	$10^{-5}s$	$100,kHz$
Sulfato de magnesio (2)	$2\times 10^{-8}s$	$200,kHz$

Sobre esta base se estima el factor de absorción en función de la frecuencia y suponiendo pH típico es con :

$\alpha = \alpha_1 \displaystyle\frac{ \nu ^2}{ \nu ^2+\nu_1^2} + \alpha_2 \displaystyle\frac{ \nu ^2}{ \nu ^2+ \nu_2 ^2} + \alpha_2 \nu ^2 + \alpha_0$

En este caso el primer termino es el que depende del ácido bórico, el segundo del sulfato de magnesio y el tercero de la ionización propia del agua. Ademas se puede comentar que no existe un efecto por la salinidad (no hay relajación por iones de sodio y/o cloro).

Mas detalles en el articulo Study of Absorption Loss Effects on Acoustic Wave Propagation in Shallow Water using Different empirical Models, Yasin Yousif Al-Aboosil, Mustafa Sami Ahmed, Nor Shahida Mohd Shah and Nor Hisham Haji Khamis

ID:(11833, 0)