Usuario:
Bombas de rotor y centrifugas
Imagen 
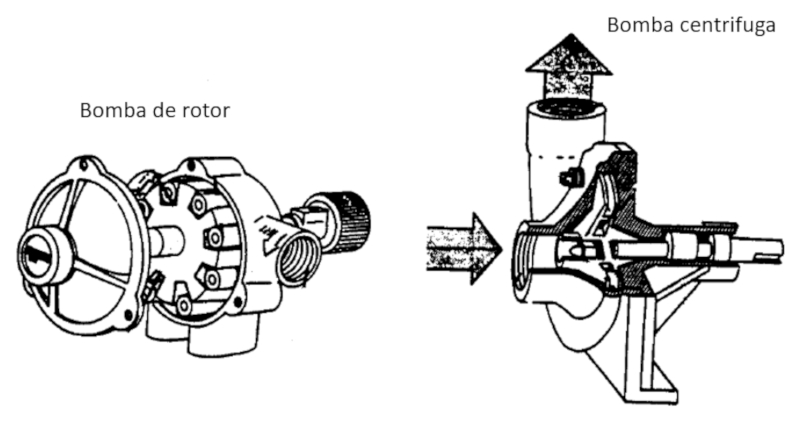
Los dos principales mecanismos sobre los que se basan las bombas son de rotor (desplazan liquido) y las centrifugas que aceleran el liquido radialmente para generar el movimiento.
ID:(12894, 0)
Comparación entre bombas
Imagen
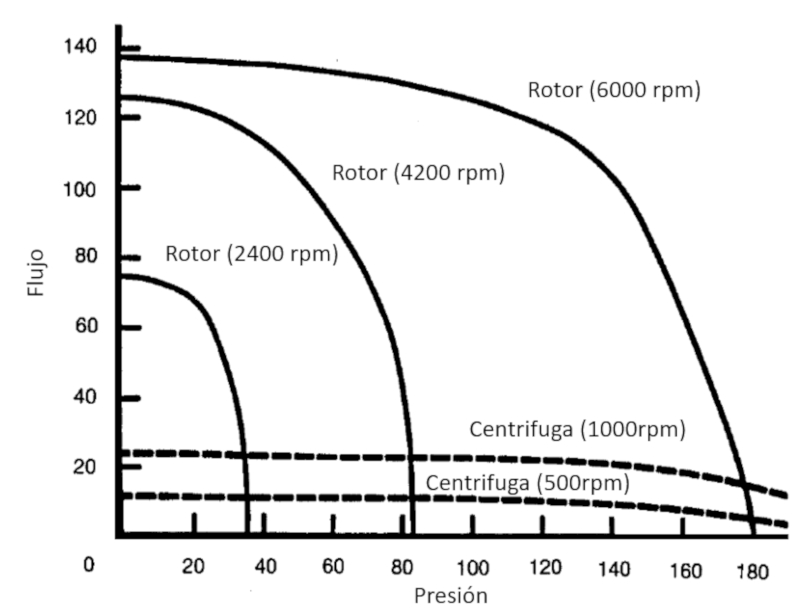
Las bombas centrifugas logran un menor flujo pero parejo sobre un mayor rango de diferencia de presiones:
ID:(12896, 0)
Ecuación de Bernoulli, variaciones
Ecuación
El diferencial de la presión ($\Delta p$) se puede calcular de la velocidad promedio ($\bar{v}$) y la diferencia de velocidad entre superficies ($\Delta v$) con la densidad ($\rho$) mediante
 $ \Delta p = - \rho \bar{v} \Delta v $ |
Para el caso de que no exista presión histrostatica la ley de Bernoulli para la densidad ($\rho$), la presión en la columna 1 ($p_1$), la presión en la columna 2 ($p_2$), la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$)
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
se puede reescribir con el diferencial de la presión ($\Delta p$)
| $ \Delta p = p_2 - p_1 $ |
y teniendo presente de que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
con
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
y
| $ \Delta v = v_2 - v_1 $ |
se tiene que
| $ \Delta p = - \rho \bar{v} \Delta v $ |
que permite ver el efecto de la melocidad promedio de un cuerpo y de la diferencia de esta entre sus superficies como se observa en un ala de avion o ave.
ID:(4835, 0)
Ley de Darcy y resistencia hidráulica
Ecuación
Darcy reescribe la ecuación de Hagen Poiseuille de modo que la diferencia de presión ($\Delta p$) es igual a la resistencia hidráulica ($R_h$) por el flujo de volumen ($J_V$):
| $ \Delta p = R_h J_V $ |
El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuación siguiente:
| $ J_V = G_h \Delta p $ |
Además, utilizando la relación para la resistencia hidráulica ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
se obtiene el resultado final:
| $ \Delta p = R_h J_V $ |
ID:(3179, 0)
Resistencia hidráulica de un tubo
Ecuación
Dado que la resistencia hidráulica ($R_h$) es igual al inverso de la conductancia hidráulica ($G_h$), podemos calcularlo a partir de la expresión de este último. De esta manera, podemos identificar parámetros relacionados con la geometría (el largo de tubo ($\Delta L$) y el radio del tubo ($R$)) y el tipo de líquido (la viscosidad ($\eta$)), que pueden ser denominados colectivamente como una resistencia hidráulica ($R_h$):
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) según la siguiente ecuación:
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
y dado que la conductancia hidráulica ($G_h$) se expresa en términos de la viscosidad ($\eta$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
podemos concluir que:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
ID:(3629, 0)
Conductividad hidráulica en paralelo
Concepto
Si se tienen tres resistencias hidráulicas $R_{h1}$, $R_{h2}$ y $R_{h3}$, la suma en serie de las resistencias será:
| $ K_{pt} = \displaystyle\sum_k K_{hk}$ |
ID:(3631, 0)