Benützer:
Bombas de rotor y centrifugas
Bild 
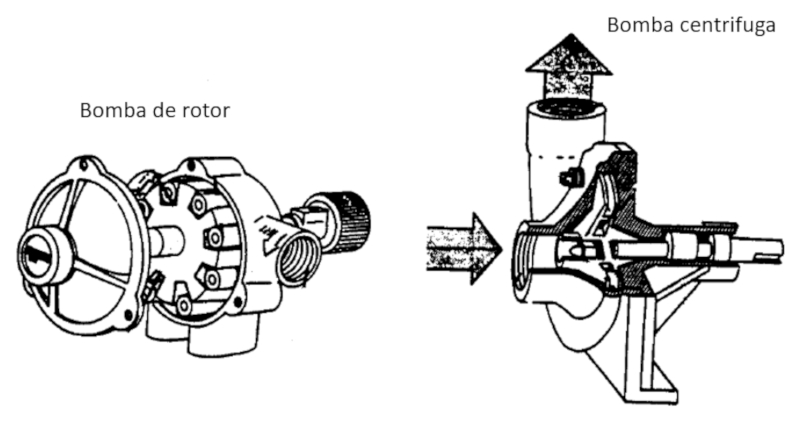
Los dos principales mecanismos sobre los que se basan las bombas son de rotor (desplazan liquido) y las centrifugas que aceleran el liquido radialmente para generar el movimiento.
ID:(12894, 0)
Comparación entre bombas
Bild
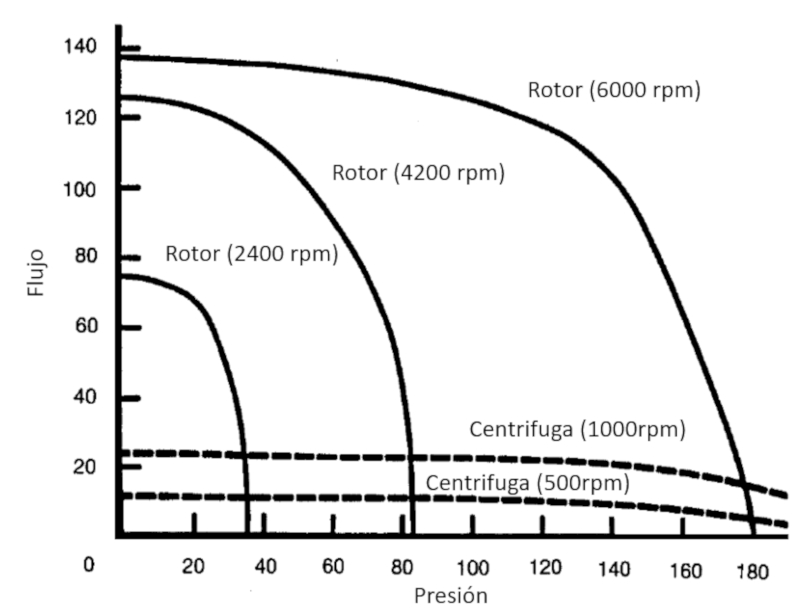
Las bombas centrifugas logran un menor flujo pero parejo sobre un mayor rango de diferencia de presiones:
ID:(12896, 0)
Bernoulli-Gleichung, Variationen
Gleichung
Die Variación de la Presión ($\Delta p$) kann aus die Durchschnittsgeschwindigkeit ($\bar{v}$) und die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) mit die Dichte ($\rho$) berechnet werden
 $ \Delta p = - \rho \bar{v} \Delta v $ |
Für den Fall, dass kein hystrostatischer Druck vorhanden ist, gilt das Bernoulli-Gesetz für die Dichte ($\rho$), die Druck in Spalte 1 ($p_1$), die Druck in Spalte 2 ($p_2$), die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) und < var>5416
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
kann mit umgeschrieben werden die Variación de la Presión ($\Delta p$)
| $ \Delta p = p_2 - p_1 $ |
und das im Hinterkopf behalten
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
mit
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
Und
| $ \Delta v = v_2 - v_1 $ |
du musst
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Dies ermöglicht es uns, den Einfluss der Durchschnittsgeschwindigkeit eines Körpers und des Unterschieds zwischen seinen Oberflächen zu sehen, wie er bei einem Flugzeug oder einem Vogelflügel beobachtet wird.
ID:(4835, 0)
Darcys Gesetz und hydraulischer Widerstand
Gleichung
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
| $ \Delta p = R_h J_V $ |
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
| $ J_V = G_h \Delta p $ |
Weiterhin, unter Verwendung der Beziehung für die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ergibt sich:
| $ \Delta p = R_h J_V $ |
ID:(3179, 0)
Hydraulischer Widerstand eines Rohres
Gleichung
Da die Hydraulic Resistance ($R_h$) dem Kehrwert von die Hydraulische Leitfähigkeit ($G_h$) entspricht, kann es aus dem Ausdruck des letzteren berechnet werden. Auf diese Weise können wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Rohrradius ($R$)) und der Art des Fluids (die Viskosität ($\eta$)) zusammenhängen und die gemeinsam als eine Hydraulic Resistance ($R_h$) bezeichnet werden können:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
Da die Hydraulic Resistance ($R_h$) gemäß der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) ausgedrückt wird:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
können wir folgern, dass:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
ID:(3629, 0)
Parallele hydraulische Leitfähigkeit
Konzept
Wenn wir drei hydraulische Widerstände $R_{h1}$, $R_{h2}$ und $R_{h3}$ haben, ist die Reihenschaltung der Widerstände:
| $ K_{pt} = \displaystyle\sum_k K_{hk}$ |
ID:(3631, 0)