Benützer:
Technische Lösung
Konzept 
Der Otto-Motor arbeitet in zwei Zyklen: dem eigentlichen Otto-Zyklus, der aus den folgenden Phasen besteht:
• Phase 1 bis 2: Adiabatische Kompression
• Phase 2 bis 3: Erwärmung
• Phase 3 bis 4: Adiabatische Expansion
• Phase 4 bis 1: Abkühlung
Zusätzlich gibt es einen Zyklus zum Entleeren der verbrannten Gase und zum Befüllen mit einer frischen Mischung.
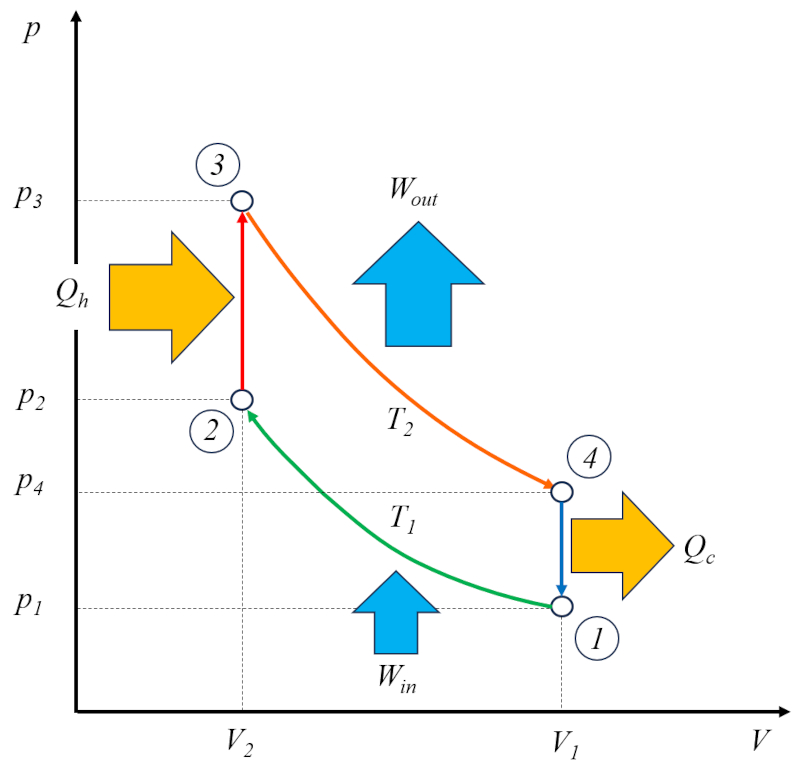
Aus diesem Grund wird er als Zweischichtmotor bezeichnet. Die Phase des Entleerens und Befüllens kann durch eine Ausgleichsmasse oder durch einen zweiten Zylinder durchgeführt werden, der außerhalb der Phase arbeitet.
Die Effizienz die Leistungsfähigkeit ($\eta$) des Motors kann mithilfe von der Otto-Kompressibilitätsfaktor ($r$) und der Adiabatischer Index ($\kappa$) mit folgender Gleichung geschätzt werden:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Kompressibilitätsfaktor $r$
Gleichung
Die Leistungsfähigkeit ($\eta$) ist letztendlich eine Funktion von der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$), und insbesondere von der Otto-Kompressibilitätsfaktor ($r$):
 $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Die adiabatische Expansion wird mithilfe der Variablen der Adiabatischer Index ($\kappa$), die Temperatur im Zustand 4 ($T_4$), die Temperatur im Zustand 3 ($T_3$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) durch die Beziehung
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
beschrieben, während die adiabatische Kompression durch die Temperatur im Zustand 1 ($T_1$) und die Temperatur im Zustand 2 ($T_2$) mithilfe der Beziehung
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
dargestellt wird. Durch Subtrahieren der zweiten Gleichung von der ersten erhalten wir
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Daraus ergibt sich die Beziehung
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Und dies ermöglicht es uns, der Otto-Kompressibilitätsfaktor ($r$) wie folgt zu definieren:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
ID:(11162, 0)
Wirkungsgrad abhängig vom Kompressibilitätsfaktor
Gleichung
Die Leistungsfähigkeit ($\eta$) kann aus der Otto-Kompressibilitätsfaktor ($r$) und der Adiabatischer Index ($\kappa$) im Fall des Otto-Zyklus berechnet werden mit:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
Die Leistungsfähigkeit ($\eta$), in Bezug auf die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$), wird mithilfe der folgenden Gleichung berechnet:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Im Falle der adiabatischen Expansion wird sie durch der Adiabatischer Index ($\kappa$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) beschrieben, gemäß der Beziehung:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Und die adiabatische Kompression wird durch die Beziehung repräsentiert:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Wenn wir die zweite Gleichung von der ersten subtrahieren, erhalten wir:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Dies führt zur Beziehung:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Dies wiederum führt zur Definition von der Otto-Kompressibilitätsfaktor ($r$) mit der folgenden Gleichung:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Mit all diesen Komponenten kann die Effizienz eines Prozesses unter Verwendung des Otto-Zyklus wie folgt berechnet werden:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
.
ID:(11163, 0)