Usuario:
Fuerza de Stokes
Ecuación 
La resistencia se define en función de la viscosidad del fluido y la velocidad de la esfera de la siguiente manera:
| $ F_v = b v $ |
Stokes calculó explícitamente la resistencia experimentada por la esfera y determinó que la viscosidad es proporcional al radio de la esfera y su velocidad, lo que lleva a la siguiente ecuación para la resistencia:
 $ F_v =6 \pi \eta r v $ |
ID:(4871, 0)
Distribuidor de líquidos
Imagen
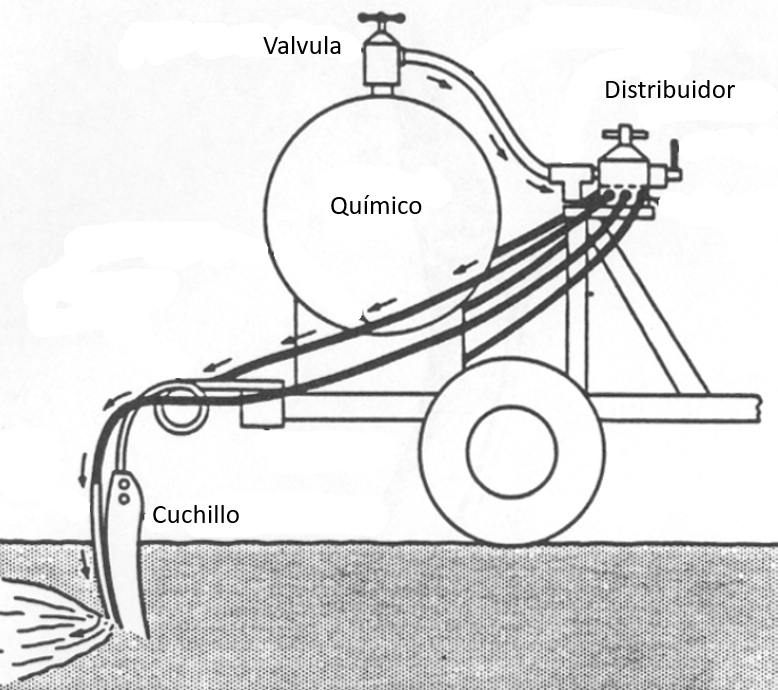
En caso de que se busca introducir el químico como liquido en el suelo se trabaja con un sistema que lleva un estanque y trabaja con un cuchillo de abre la tierra para depositar el liquido:
ID:(12893, 0)
Ley de Darcy y resistencia hidráulica
Ecuación
Darcy reescribe la ecuación de Hagen Poiseuille de modo que la diferencia de presión ($\Delta p$) es igual a la resistencia hidráulica ($R_h$) por el flujo de volumen ($J_V$):
| $ \Delta p = R_h J_V $ |
El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuación siguiente:
| $ J_V = G_h \Delta p $ |
Además, utilizando la relación para la resistencia hidráulica ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
se obtiene el resultado final:
| $ \Delta p = R_h J_V $ |
ID:(3179, 0)
Resistencia hidráulica de un tubo
Ecuación
Dado que la resistencia hidráulica ($R_h$) es igual al inverso de la conductancia hidráulica ($G_h$), podemos calcularlo a partir de la expresión de este último. De esta manera, podemos identificar parámetros relacionados con la geometría (el largo de tubo ($\Delta L$) y el radio del tubo ($R$)) y el tipo de líquido (la viscosidad ($\eta$)), que pueden ser denominados colectivamente como una resistencia hidráulica ($R_h$):
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) según la siguiente ecuación:
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
y dado que la conductancia hidráulica ($G_h$) se expresa en términos de la viscosidad ($\eta$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
podemos concluir que:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
ID:(3629, 0)