Usuario:
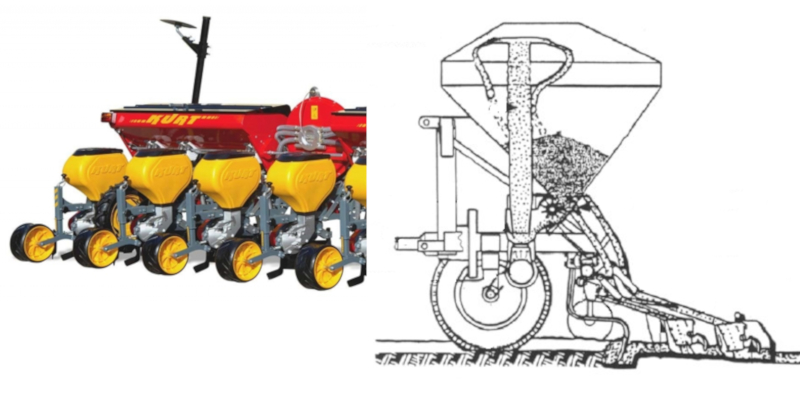
Tasa de plantación de semillas
Ecuación 
El plantar de semillas se puede modelar como un flujo de partículas en que la tasa
 $ R_s =\displaystyle\frac{ Q \rho }{ w v }$ |
ID:(12839, 0)
Plantador centrifugo
Imagen
La semillas pueden ser también distribuidas con un mecanismo centrifugo para su lanzamiento:
ID:(12899, 0)
Velocidad tangencial
Ecuación
Si se divide el camino expresado como arco de un circulo se tendrá que con es
| $ \Delta s=r \Delta\theta $ |
por el tiempo transcurrido
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y como la velocidad angular con es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
se tiene con la relación
| $ v_t = r \omega $ |
ID:(10968, 0)
Camino con aceleración constante y tiempo inicial cero
Ecuación
En el caso de que se asuma que la aceleración inicial es constante y tiempo inicial nulo la ecuación de la posición
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
En el caso de que se asuma que el tiempo inicial es nulo\\n\\n
$t_0=0$
la ecuación de la posición
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
ID:(4360, 0)
Distancia horizontal recorrida
Ecuación
El objeto recorre en un tiempo ($t$) a una velocidad horizontal inicial ($v_{0x}$) Una posición en el eje x ($x$) igual a
| $ x = v_{0x} t $ |
La posición ($s$) recorrido con velocidad constante ($v_0$) con la posición inicial ($s_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) es
| $ s = s_0 + v_0 ( t - t_0 )$ |
Por lo tanto, si el movimiento se inicia en el origen ($s_0=0$) al comienzo del tiempo ($t_0=0$), el movimiento se describe con $x=s$ y $v_0=v_{0x}$.
| $ x = v_{0x} t $ |
ID:(10930, 0)
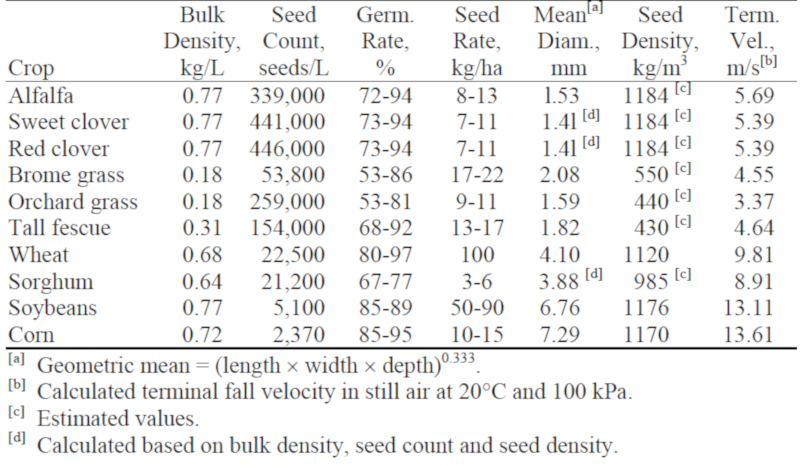
Datos de sembrado
Imagen
Los parámetros claves para la plantación se dan como ejemplo para algunas especies
ID:(12841, 0)