User:
Caída libre de la fruta
Equation 
Para cosechar fruta existe la posibilidad de liberarla y capturarla en pleno vuelo. Para ello se dispone del tiempo que se puede calcular de
 $S = \displaystyle\frac{v_t^2}{g}\ln(\cosh\displaystyle\frac{gt}{v_t})$ |
ID:(12870, 0)
Resistance force
Equation
The resistance force ($F_W$) kann mit the density ($\rho$), the coefficient of resistance ($C_W$), the total object profile ($S_p$) und the speed with respect to the medium ($v$) entsprechend berechnet werden folgende Formel:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Similarly to how the equation for the lift force ($F_L$) was derived using the density ($\rho$), the coefficient of lift ($C_L$), the surface that generates lift ($S_w$), and the speed with respect to the medium ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
in this analogy, what corresponds to the surface that generates lift ($S_w$) will be equivalent to the total object profile ($S_p$) and the coefficient of lift ($C_L$) to the coefficient of resistance ($C_W$), thus the resistance force ($F_W$) is calculated:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
The drag coefficient is measured and, in turbulent flows over aerodynamic bodies, values are generally found around 0.4.
ID:(4418, 0)
Fuerza gravitacional sin sustentación
Equation
Si se resta la fuerza de flotación de la fruta en el aire la fuerza gravitacional será
| $ F_g = m_b g \displaystyle\frac{ \rho_b - \rho }{ \rho_b }$ |
ID:(12876, 0)
Velocidad relativa de caída
Equation
Si se iguala la fuerza de resistencia aerodinámica con la de gravedad menos la de flotación se obtiene la velocidad de caída relativa como
| $ v_r ^2 = 2 g m_b \displaystyle\frac{ \rho_b - |
O sea que una fruta en una corriente de esta misma velocidad flotara y impurezas serán arrastradas con la corriente. El sistema también se puede usar para separar calibres.
ID:(12877, 0)
Angular frequency for a physical pendulum
Equation
Regarding the physical pendulum:
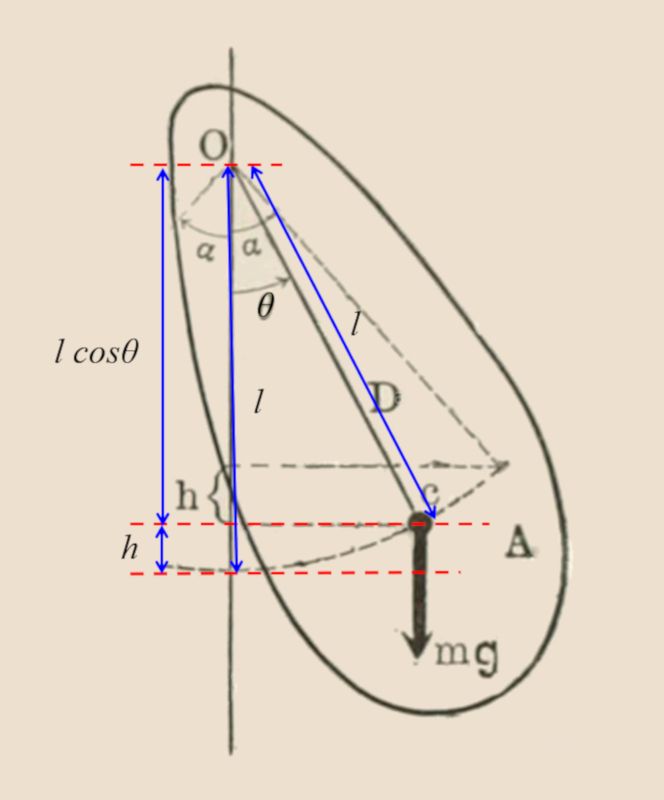
The energy is given by:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
As a result, the angular frequency is:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
Given that the kinetic energy of the physical pendulum with moment of inertia $I$ and angular velocity $\omega$ is represented by
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
and the gravitational potential energy is given by
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
where $m$ is mass, $l$ is string length, $\theta$ is the angle, and $g$ is angular acceleration, the energy equation can be expressed as
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
As the period is defined as
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
we can determine the angular frequency as
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
ID:(4517, 0)