Force de résistance
Équation 
A force de résistance (F_W) peut être calculé en utilisant a densité (\rho), le coefficient de résistance (C_W), le profil total de l'objet (S_p) et a vitesse par rapport au milieu (v) selon le formule suivante :
De manière similaire à la façon dont l'équation pour a force de levage (F_L) a été dérivée en utilisant a densité (\rho), le coefficient de portance (C_L), a surface génératrice de portance (S_w) et a vitesse par rapport au milieu (v)
| F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2 |
dans cette analogie, ce qui correspond à A surface génératrice de portance (S_w) sera équivalent à Le profil total de l'objet (S_p) et le coefficient de portance (C_L) à Le coefficient de résistance (C_W), ce qui permet de calculer a force de résistance (F_W) :
| F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2 |
Le coefficient de traînée est mesuré et, dans les écoulements turbulents sur les corps aérodynamiques, les valeurs sont généralement autour de 0.4.
ID:(4418, 0)
Fréquence angulaire pour un pendule physique
Équation 
En ce qui concerne le pendule physique:
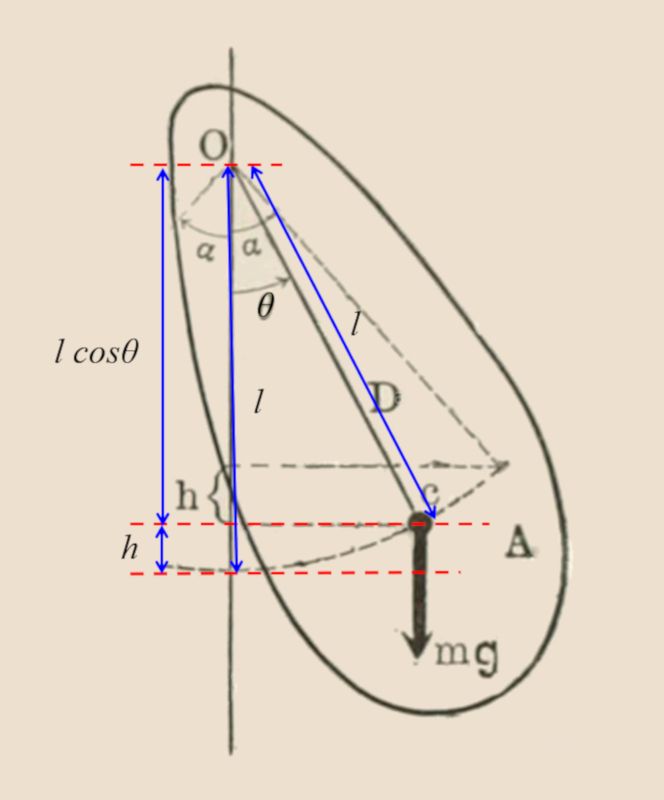
L'énergie est donnée par :
E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2
Par conséquent, la fréquence angulaire est:
Étant donné que l'énergie cinétique du pendule physique avec un moment d'inertie I et une vitesse angulaire \omega est représentée par
et l'énergie potentielle gravitationnelle est donnée par
où m est la masse, l est la longueur de la corde, \theta est l'angle et g est l'accélération angulaire, l'équation d'énergie peut être exprimée comme
E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2
Comme la période est définie comme
T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}
nous pouvons déterminer la fréquence angulaire comme suit :
ID:(4517, 0)
