Utilizador:
Força de resistência
Equação 
La força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) de acordo com o seguinte fórmula:
 $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
De maneira semelhante à forma como a equação para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) será equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no cálculo de la força de resistência ($F_W$):
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
O coeficiente de arrasto é medido e, em fluxos turbulentos sobre corpos aerodinâmicos, geralmente se obtêm valores em torno de 0.4.
ID:(4418, 0)
Frequência angular para um pêndulo físico
Equação
No caso do pêndulo físico:
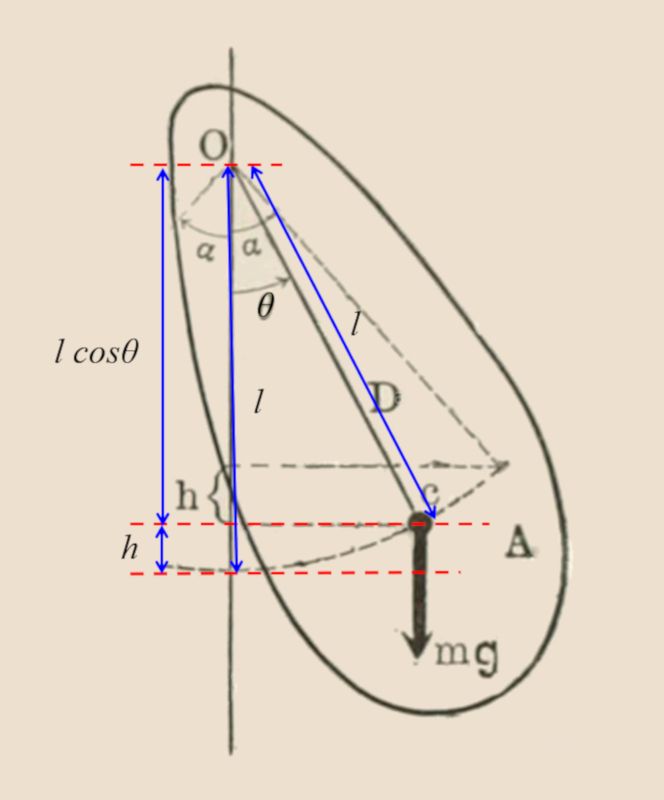
A energia é dada por:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Consequentemente, a frequência angular é:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
Dado que a energia cinética do pêndulo físico com momento de inércia $I$ e velocidade angular $\omega$ é representada por
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
e a energia potencial gravitacional é dada por
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
onde $m$ é a massa, $l$ é o comprimento da corda, $\theta$ é o ângulo e $g$ é a aceleração angular, a equação de energia pode ser expressa como
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Como o período é definido como
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
podemos determinar a frequência angular da seguinte forma:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
ID:(4517, 0)