Benützer: 
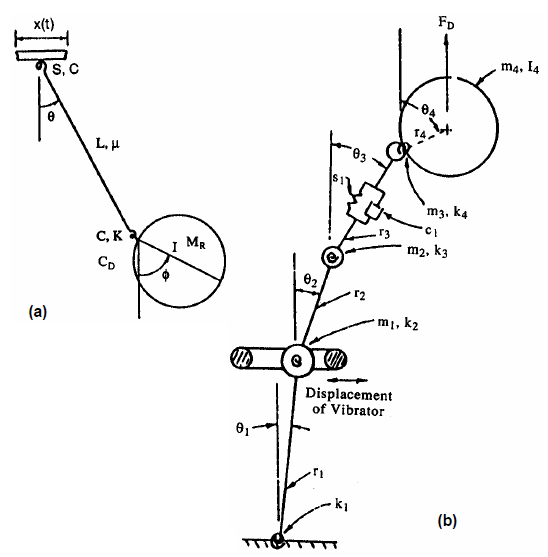
Caída libre de la fruta
Gleichung 
Para cosechar fruta existe la posibilidad de liberarla y capturarla en pleno vuelo. Para ello se dispone del tiempo que se puede calcular de
 $S = \displaystyle\frac{v_t^2}{g}\ln(\cosh\displaystyle\frac{gt}{v_t})$ |
ID:(12870, 0)
Widerstandskraft
Gleichung
Die Widerstandskraft ($F_W$) se puede utilizar con die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) y die Geschwindigkeit in Bezug auf das Medium ($v$) de acuerdo con la siguiente fórmula:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Ähnlich wie die Gleichung für die Auftriebskraft ($F_L$) unter Verwendung von die Dichte ($\rho$), der Koeffizient Fahrstuhl ($C_L$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Geschwindigkeit in Bezug auf das Medium ($v$) abgeleitet wurde
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
entspricht in dieser Analogie das, was die Oberfläche, die Auftrieb erzeugt ($S_w$) entspricht, der Gesamtobjektprofil ($S_p$) und der Koeffizient Fahrstuhl ($C_L$) entspricht der Widerstandskoeffizient ($C_W$), woraus die Widerstandskraft ($F_W$) berechnet wird:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Der Widerstandsbeiwert wird gemessen und bei turbulenten Strömungen über aerodynamischen Körpern werden üblicherweise Werte um 0,4 ermittelt.
ID:(4418, 0)
Fuerza gravitacional sin sustentación
Gleichung
Si se resta la fuerza de flotación de la fruta en el aire la fuerza gravitacional será
| $ F_g = m_b g \displaystyle\frac{ \rho_b - \rho }{ \rho_b }$ |
ID:(12876, 0)
Velocidad relativa de caída
Gleichung
Si se iguala la fuerza de resistencia aerodinámica con la de gravedad menos la de flotación se obtiene la velocidad de caída relativa como
| $ v_r ^2 = 2 g m_b \displaystyle\frac{ \rho_b - |
O sea que una fruta en una corriente de esta misma velocidad flotara y impurezas serán arrastradas con la corriente. El sistema también se puede usar para separar calibres.
ID:(12877, 0)
Winkelfrequenz für ein physikalisches Pendel
Gleichung
Im Fall des physikalischen Pendels:
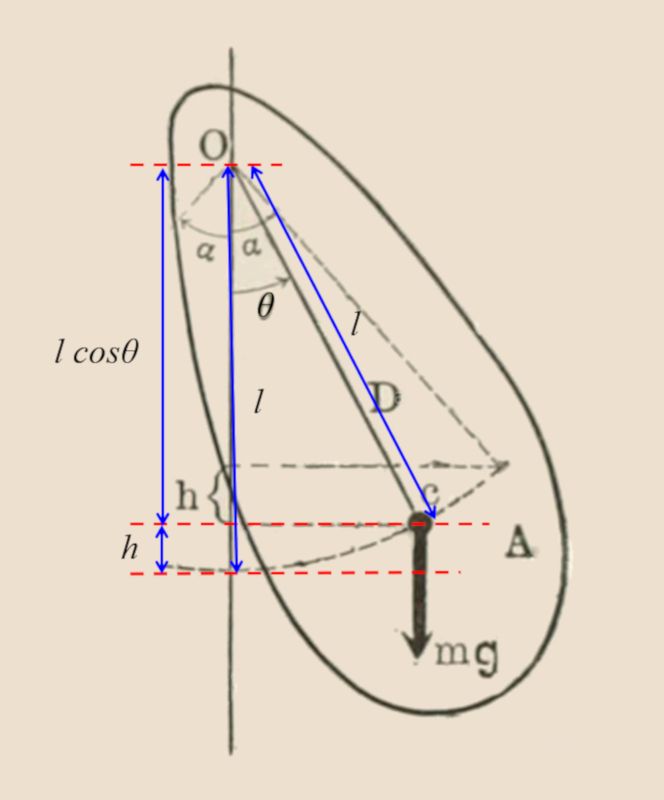
Die Energie ist gegeben durch:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Daraus ergibt sich die Winkelgeschwindigkeit:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
Angesichts der kinetischen Energie des physikalischen Pendels mit Trägheitsmoment $I$ und Winkelgeschwindigkeit $\omega$, die durch
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
repräsentiert wird, sowie der potenziellen Gravitationsenergie, die durch
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
gegeben ist, wobei $m$ die Masse, $l$ die Seillänge, $\theta$ der Winkel und $g$ die Winkelbeschleunigung sind, kann die Energiegleichung wie folgt ausgedrückt werden:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Da die Periode definiert ist als
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
können wir die Winkelgeschwindigkeit wie folgt bestimmen:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
ID:(4517, 0)