Benützer: 
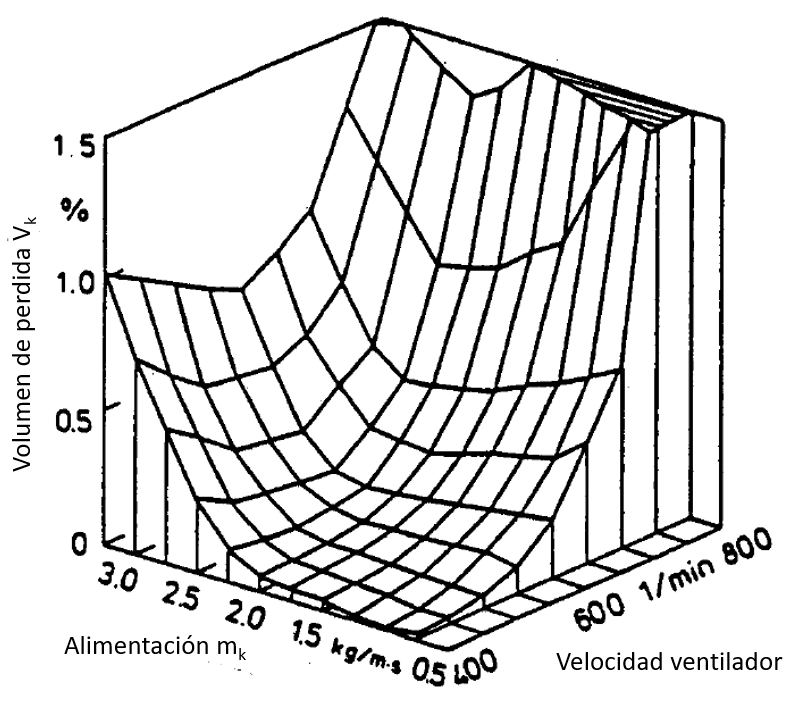
Modelo de difusión para la separación
Gleichung 
Para modelar el proceso de separación se puede asumir un proceso de difusión que se describe por la ley de Fick. En este caso se tiene que el flujo de granos
 Q_g =- D \displaystyle\frac{ A }{ L_g }( C_2 - C_1 ) |
en que
ID:(12863, 0)
Ecuación en volumen
Gleichung
En base al modelo de difusión se puede establecer una ecuación para el volumen de grano en base al flujo de granos
| Q_g = \displaystyle\frac{ dV_g }{ dt } |
ID:(12864, 0)
Diferencia de concentraciones
Gleichung
La diferencia de concentraciones se puede estimar en función de los volúmenes con grano en relación al volumen del material sin grano (MOG= Material out of Grain) como
| C_2 - C_1 = \displaystyle\frac{ V_g }{ V_{MOG} } |
ID:(12865, 0)
Ecuación para el volumen de granos
Gleichung
Con la ley de Fick, el flujo de granos y la estimación de la diferencia de concentraciones se obtiene la ecuación
| \displaystyle\frac{ dV_g }{ dt } = -D\displaystyle\frac{ W L }{ L_d }\displaystyle\frac{ V_g }{ V_{MOG} } |
ID:(12866, 0)
Volumen de granos en el tiempo
Gleichung
La solución de la ecuación del volumen de granos es de la forma
| V_{gf} = V_{gi} e^{- D W L t / L_g V_{MOG} } |
ID:(12867, 0)
Tasa de alimentación de MOG
Gleichung
La tasa de alimentación de MOG nos permite estimar el tiempo ya que
| \dot{ m } =\displaystyle\frac{ V_{MOG} }{ t } |
ID:(12868, 0)
Masa final de granos
Gleichung
Como la masa de granos es proporcional al volumen de granos se tiene que la solución del volumen de granos con la tasa MOG da un volumen de granos de
| G_f = G_i e^{ D W \rho_{MOG} L / L_g \dot{m} } |
ID:(12869, 0)
