Epidemia SARS 2003 en Hong Kong
Imagen 
En el 2003 se produce en China un brote de SARS (Severe acute respiratory syndrome) que se propaga a Hong Kong y luego al mundo entero. En el siguiente mapa se ve la cantidad de casos en los distintos países:
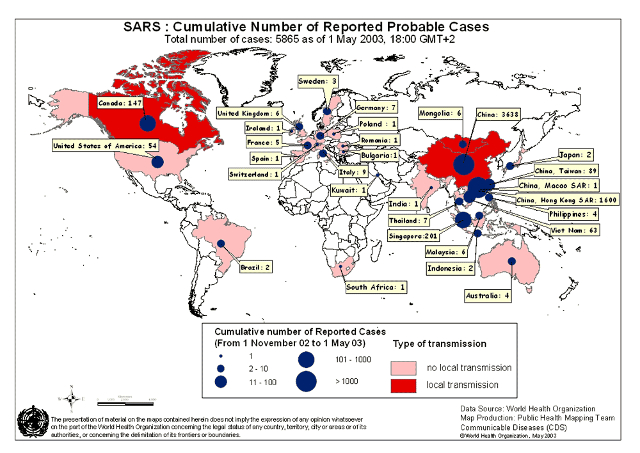
ID:(9662, 0)
Modelo SIR para describir SARS 2003 en Hong Kong
Imagen 
Si se observan los susceptibles, infectados y 'recuperados' (que se sanan o mueren) se observan las típicas curvas del modelo SIR:
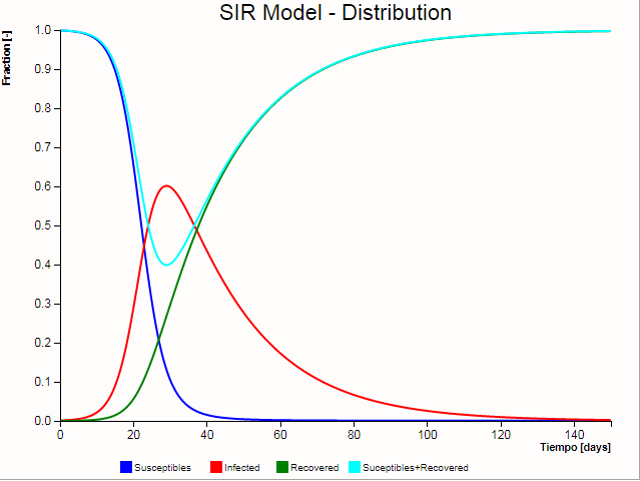
ID:(9663, 0)
Análisis epidemia SARS 2003 en Hong Kong
Imagen 
Si se estudia los datos de la WHO para la epidemia de SARS en 2003 en Hong Kong se puede estimar el numero actual de infectados

\\n\\nAun cuando no se tiene la sección del inicio se observa el máximo típico del número de infectados cuando se comienza a controlar estos y se da que\\n\\n
\displaystyle\frac{dS}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I=0
\\n\\npor lo que los susceptibles en dicho punto alcanzan\\n\\n
S=\displaystyle\frac{\gamma}{\beta C}N
ID:(8202, 0)
Determinación de Parametros SARS 2003 en Hong Kong
Imagen 
Si se estudia la forma como descienden los infectados se ve que al avanzar el tiempo debe dominar el termino gamma ya que es el que reduce el volumen total que describe el primer termino. Por ello se tiene que para tiempos en que la epidemia esta bajo control\\n\\n
\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I\sim-\gamma I
\\n\\nEn ese caso la solución asintomática es de la forma\\n\\n
I(t) \propto e^{-\gamma t}
lo que se aprecia en la curva de los infectados existentes para el caso SARS 2003 en Hong Kong. Por ello se puede hacer un ajuste por mínimos cuadrados de la parte final de la curva
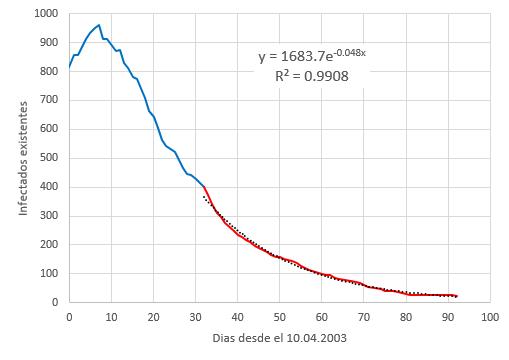
\\n\\nobteniendo se que el factor
\tau=\displaystyle\frac{1}{\gamma}\sim 20.8,dias
Si además asumimos que cada persona se reúne a diario con del orden de 30 personas, se tendría que el factor
ID:(8203, 0)
Tasa de Mortalidad
Imagen 
La mortalidad mundial es distinta según el país del mundo. Mientras en países desarrollados llega a valores inferiores a 5 muertes por cada 1000 habitantes y año en países subdesarrollados llega a mas de 11:
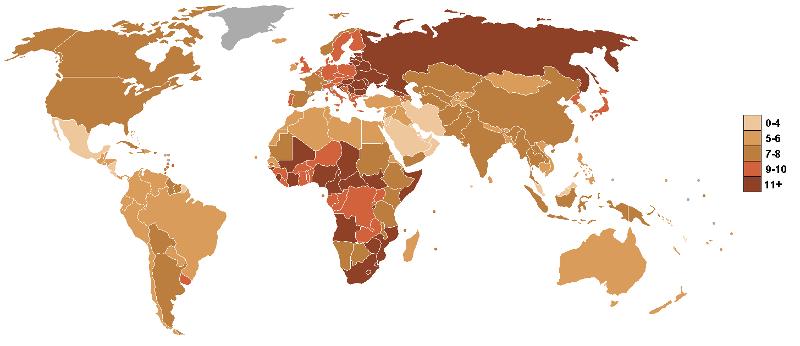
wikicommons, Autor: UN
El factor que exige el modelo es la probabilidad por día de que una persona muera. Es decir se debe tomar el número de muertes diarias (casos favorables a la hipótesis) y dividirla por el número de personas vivas. De esta forma si se multiplica el factor
ID:(8217, 0)
Tasa de Natalidad
Imagen 
La natalidad mundial es distinta según el país del mundo. Mientras en países desarrollados llega a valores inferiores a 15 nacimientos por cada 1000 habitantes y año en países subdesarrollados llega hasta 46:
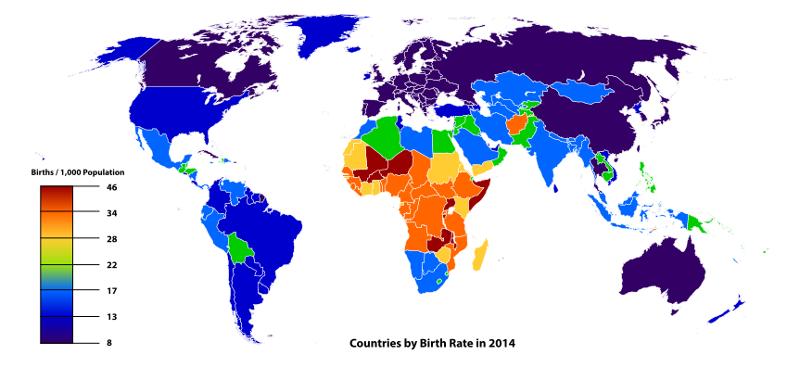
wikicommons, Autor: Ali Zifan
El factor que exige el modelo es la probabilidad por día de que una persona nazca. Es decir se debe tomar el número de nacimientos diarias (casos favorables a la hipótesis) y dividirla por el número de personas vivas. De esta forma si se multiplica el factor
ID:(8216, 0)
Simulador SIR
Php 
El simulador SIR permite definir los parámetros de un modelo SIR y observar su evolución:
ID:(9656, 0)
Simulador SEIR
Php 
El simulador SEIR permite definir los parámetros de un modelo SEIR y observar su evolución:
ID:(9657, 0)
Simulador SEIR-largo plazo
Php 
El simulador SEIR-largo plazo permite definir los parámetros de un modelo SEIR y observar su evolución:
ID:(9658, 0)
Simulador SARS - ajuste de un Modelo SEIR
Php 
El presente simulador contiene los datos de la epidemia de SARS para el caso de Hong Kong y permite buscar los parámetros de un modelo SEIR ajustando las curvas a los valores reales:
ID:(9659, 0)
