Storyboard

>Modell

ID:(571, 0)

Bild

>Top

Im Jahr 2003 kommt es in China zu einem Ausbruch von SARS (schweres akutes respiratorisches Syndrom), der sich auf Hongkong und dann auf die ganze Welt ausbreitet. Die folgende Karte zeigt die Anzahl der Fälle in den verschiedenen Ländern:

ID:(9662, 0)

Bild

>Top

Wenn die anfälligen, infizierten und 'erholten' (die heilen oder sterben) beobachtet werden, werden die typischen Kurven des SIR-Modells beobachtet:

ID:(9663, 0)

Bild

>Top

Wenn die WHO-Daten für die SARS-Epidemie im Jahr 2003 in Hongkong untersucht werden, kann die aktuelle Anzahl infizierter I geschätzt werden, wenn die Anzahl der akkumulierten Infizierten von der akkumulierten Anzahl der geborgenen und toten Menschen abgezogen wird. Das Ergebnis ist die folgende Grafik:

\\n\\nSelbst wenn Sie nicht über den Anfangsabschnitt verfügen, können Sie das für die Anzahl der Infizierten typische Maximum sehen, wenn Sie mit der Kontrolle beginnen, und dies ist gegeben\\n\\n

$\displaystyle\frac{dS}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I=0$

\\n\\nso dass diejenigen, die an diesem Punkt anfällig sind, erreichen\\n\\n

$S=\displaystyle\frac{\gamma}{\beta C}N$

ID:(8202, 0)

Bild

>Top

Wenn Sie die Art und Weise untersuchen, in der die Infizierten absteigen, wird festgestellt, dass im Laufe der Zeit der Begriff Gamma dominieren muss, da er das durch den ersten Begriff beschriebene Gesamtvolumen reduziert. Deshalb ist es notwendig, wenn die Epidemie unter Kontrolle ist\\n\\n

$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I\sim-\gamma I$

\\n\\nIn diesem Fall hat die asymptomatische Lösung die Form\\n\\n

$I(t) \propto e^{-\gamma t}$

Was ist in der bestehenden infizierten Kurve für den Fall SARS 2003 in Hongkong zu sehen? Daher kann eine minimale quadratische Anpassung des letzten Teils der Kurve vorgenommen werden

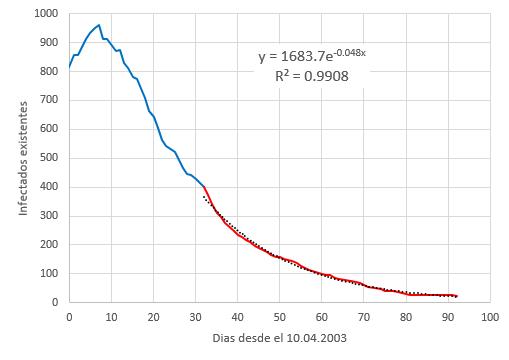
\\n\\nErhalten, dass der Faktor \gamma in der Größenordnung von 0,048 1 / Tag liegen muss. Dies entspricht einer durchschnittlichen Zeit von der Infektion bis zur Genesung von\\n\\n

$\tau=\displaystyle\frac{1}{\gamma}\sim 20.8,dias$

Wenn wir auch davon ausgehen, dass sich jede Person täglich in der Größenordnung von 30 Personen trifft, müsste der \beta -Faktor geschätzt werden, damit die vom Simulator erzeugte Kurve der von der WHO gemessenen Kurve ähnelt.

ID:(8203, 0)

Bild

>Top

Die Weltsterblichkeit ist je nach Land der Welt unterschiedlich. Während es in Industrieländern Werte unter 5 Todesfällen pro 1000 Einwohner erreicht und in unterentwickelten Ländern jährlich mehr als 11:

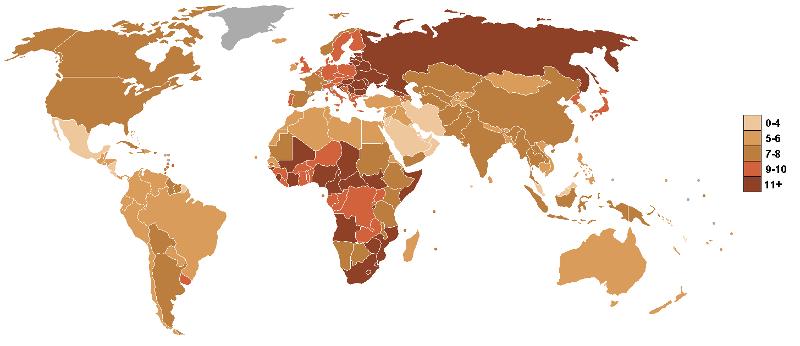
Der vom Modell geforderte Faktor ist die Wahrscheinlichkeit pro Tag, dass eine Person stirbt. Mit anderen Worten, die Anzahl der täglichen Todesfälle (für die Hypothese günstige Fälle) muss genommen und durch die Anzahl der lebenden Personen geteilt werden. Auf diese Weise wird die Anzahl dieser Faktoren erhalten, die wahrscheinlich an einem Tag aus einem anderen Grund sterben werden, wenn der Faktor \mu_d mit der Population multipliziert wird, die anfällig, latent, infiziert oder wiederhergestellt ist.

ID:(8217, 0)

Bild

>Top

Die Weltgeburt ist je nach Land der Welt unterschiedlich. Während es in Industrieländern Werte unter 15 Geburten pro 1000 Einwohner und in unterentwickelten Ländern Jahr 46 erreicht, erreicht es 46:

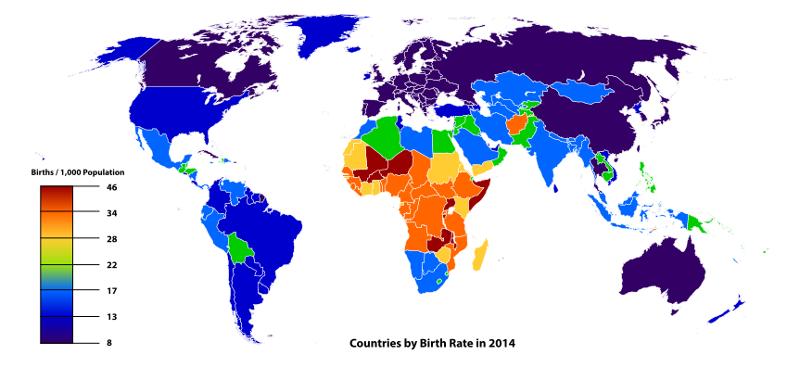
Der vom Modell geforderte Faktor ist die Wahrscheinlichkeit pro Tag, dass eine Person geboren wird. Mit anderen Worten, die Anzahl der täglichen Geburten (Fälle, die für die Hypothese günstig sind) muss genommen und durch die Anzahl der lebenden Personen geteilt werden. Auf diese Weise wird die Anzahl dieser Faktoren, die wahrscheinlich an einem Tag geboren werden, erhalten, wenn der Faktor \mu_b mit der Bevölkerung multipliziert wird.

ID:(8216, 0)

Php

>Top

Der SIR-Simulator ermöglicht es, die Parameter eines SIR-Modells zu definieren und seine Entwicklung zu beobachten:

ID:(9656, 0)

Php

>Top

Der SEIR-Simulator ermöglicht es, die Parameter eines SEIR-Modells zu definieren und seine Entwicklung zu beobachten:

ID:(9657, 0)

Php

>Top

Der SEIR-Langzeitsimulator ermöglicht es, die Parameter eines SEIR-Modells zu definieren und seine Entwicklung zu beobachten:

ID:(9658, 0)

Php

>Top

Dieser Simulator enthält die SARS-Epidemiedaten für den Fall Hongkong und ermöglicht die Suche nach den Parametern eines SEIR-Modells durch Anpassen der Kurven an die tatsächlichen Werte:

ID:(9659, 0)