Spezifische Mortalität mit Malaria
Bild 
Die spezifische Mortalität einer Person mit Malaria zeigt, dass es sich um eine Krankheit handelt, die hauptsächlich Kinder und ältere Menschen befällt. Die beigefügte Grafik aus der Studie ['Wie viele Jahre Leben könnten gerettet werden, wenn Malaria aus einem hyperendemischen Gebiet in Nordghana beseitigt würde?'] (Http://www.gphysics.net/downloads/medicine/Bookshelf_NBK1712.pdf) Ayaga A. Bawah und Fred N. Binka zeigen die Sterblichkeit nach Alter mit und ohne Malaria:
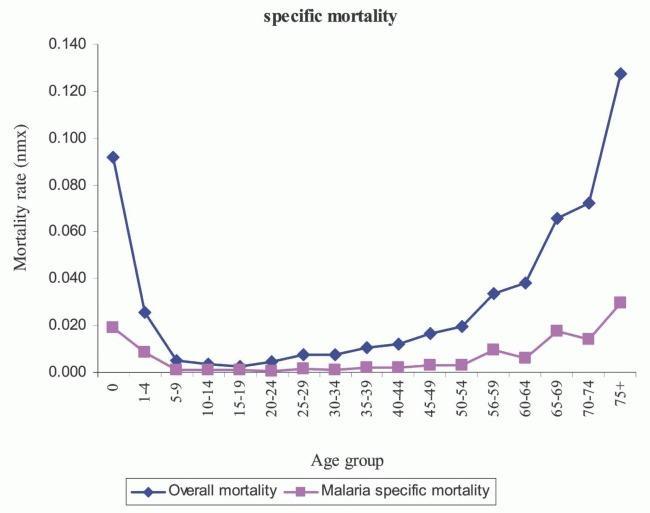
ID:(8215, 0)
Lebenserwartung mit Malaria
Bild 
Die durchschnittliche Lebenserwartung einer Person mit Malaria verringert sich im Durchschnitt um ungefähr 10 Jahre. Die beigefügte Grafik aus der Studie ['Wie viele Jahre Leben könnten gerettet werden, wenn Malaria aus einem hyperendemischen Gebiet in Nordghana beseitigt würde?'] (Http://www.gphysics.net/downloads/medicine/Bookshelf_NBK1712.pdf) Ayaga A. Bawah und Fred N. Binka zeigen die Lebenserwartung nach Alter mit und ohne Malaria:

ID:(8214, 0)
Statistik der Mücken- und Bisspopulationen
Bild 
In dem Artikel ['Die Übertragungseffizienz von Mensch zu Mücke steigt, wenn Malaria kontrolliert wird'] (http://www.gphysics.net/downloads/medicine/Churcher_et_al-2015-Nature_Communications.pdf) von Thomas S. Churcher, Jean- Francois Trape und Anna Cohuet in Nature Communications, veröffentlicht am 19. Januar 2015, betrachten die im Bild unten gezeigten Kurven:
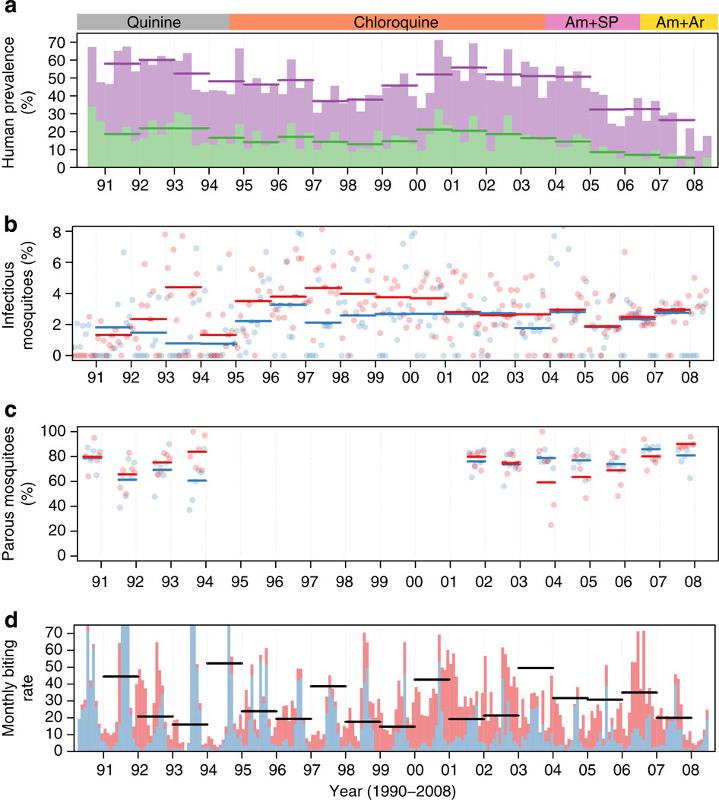
Wir retten, dass der Anteil der Mücken
Andererseits werden ungefähr 30 Bisse pro Monat beobachtet. Daher liegt die Wahrscheinlichkeit eines täglichen Bisses
Wenn Sie über Maßnahmen nachdenken, können Sie die Jahre untersuchen, in denen die Anzahl der Bisse zurückgegangen ist, und die Ursache dafür ermitteln. Wenn beispielsweise festgestellt würde, dass in einem Jahr der Dürre die Rate sinkt, könnte der Schluss gezogen werden, dass mit Entwässerungsmaßnahmen Gebiete getrocknet werden können, in denen Mücken mit Malaria leben. In diesem Fall können die Daten dieser günstigen Jahre herangezogen werden, um einen Datensatz zu bestimmen, der im Falle von Maßnahmen angegeben würde. Auf diese Weise würde eine Reduzierung von 30 bis 15 Bissen pro Monat zu Maßnahmen führen, bei denen die Wahrscheinlichkeit, gebissen zu werden, von 1 / Tag (30/30) auf 0,5 / Tag (15/30) sinkt.
Hinweis: Es ist wichtig zu beachten, dass der Faktor
ID:(8199, 0)
Abschätzung der menschlichen Ansteckungswahrscheinlichkeiten
Gleichung 
Wenn die asymptotische Situation einer Population von Menschen mit Malaria bekannt ist, können die Gleichungen verwendet werden
| i_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{p_bp_V(\gamma+\Lambda p_bp_I)} |
und
| v_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{\Lambda p_bp_I(\mu+p_bp_V)} |
um
| p_i=\displaystyle\frac{\gamma i}{(1-i)p_b v \Lambda} |
ID:(8211, 0)
Abschätzung der Ansteckungswahrscheinlichkeiten von Mücken
Gleichung 
Wenn die asymptotische Situation einer Population von Menschen mit Malaria bekannt ist, können die Gleichungen verwendet werden
| i_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{p_bp_V(\gamma+\Lambda p_bp_I)} |
und
| v_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{\Lambda p_bp_I(\mu+p_bp_V)} |
um
| p_v=\displaystyle\frac{\mu v}{p_b i(1-v)} |
ID:(8212, 0)
Länderstatistik
Beschreibung 
Bevölkerung:
Jahr | Krank | Todesfälle
: -----: |: -------: |: ---------:
2000 | 3349528 | 6108 |
2001 | 3044844 | 1717 |
2002 | 3140893 | 2376 |
2003 | 3552896 | 2103 |
2004 | 3416033 | 1575 |
2005 | 3452969 | 2037 |
2006 | 3511452 | 3125 |
2007 | 3123147 | 4622 |
2008 | 3200147 | 3889 |
2009 | 3694671 | 3378 |
2010 | 3849536 | 3859 |
2011 | 4154261 | 3259 |
2012 | 10676731 | 2855 |
2013 | 7200797 | 2506 |
2014 | 8453557 | 2200 |
ID:(9664, 0)
Wahrscheinlichkeitsschätzung
Beschreibung 
Wenn angenommen wird, dass die Anzahl der Bisse eins pro Tag beträgt (
| p_i=\displaystyle\frac{\gamma i}{(1-i)p_b v \Lambda} |
dass
| p_v=\displaystyle\frac{\mu v}{p_b i(1-v)} |
dass
ID:(8213, 0)
Malaria Simulator
Php 
Der Simulator für den Fall von Malaria ermöglicht es, mit den verschiedenen Parametern zu experimentieren und zu beobachten, wie sich die Populationen infizierter Menschen und Mücken entwickeln:
ID:(9660, 0)
