Storyboard

>Modell

ID:(1221, 0)

Bild

>Top

Im Jahr 2003 kommt es in China zu einem Ausbruch von SARS (schweres akutes respiratorisches Syndrom), der sich auf Hongkong und dann auf die ganze Welt ausbreitet. Die folgende Karte zeigt die Anzahl der Fälle in den verschiedenen Ländern:

ID:(9662, 0)

Php

>Top

Dieser Simulator enthält die SARS-Epidemiedaten für den Fall Hongkong und ermöglicht die Suche nach den Parametern eines SEIR-Modells durch Anpassen der Kurven an die tatsächlichen Werte:

ID:(9659, 0)

Bild

>Top

Wenn die WHO-Daten für die SARS-Epidemie im Jahr 2003 in Hongkong untersucht werden, kann die aktuelle Anzahl infizierter I geschätzt werden, wenn die Anzahl der akkumulierten Infizierten von der akkumulierten Anzahl der geborgenen und toten Menschen abgezogen wird. Das Ergebnis ist die folgende Grafik:

\\n\\nSelbst wenn Sie nicht über den Anfangsabschnitt verfügen, können Sie das für die Anzahl der Infizierten typische Maximum sehen, wenn Sie mit der Kontrolle beginnen, und dies ist gegeben\\n\\n

$\displaystyle\frac{dS}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I=0$

\\n\\nso dass diejenigen, die an diesem Punkt anfällig sind, erreichen\\n\\n

$S=\displaystyle\frac{\gamma}{\beta C}N$

ID:(8202, 0)

Bild

>Top

Wenn Sie die Art und Weise untersuchen, in der die Infizierten absteigen, wird festgestellt, dass im Laufe der Zeit der Begriff Gamma dominieren muss, da er das durch den ersten Begriff beschriebene Gesamtvolumen reduziert. Deshalb ist es notwendig, wenn die Epidemie unter Kontrolle ist\\n\\n

$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I\sim-\gamma I$

\\n\\nIn diesem Fall hat die asymptomatische Lösung die Form\\n\\n

$I(t) \propto e^{-\gamma t}$

Was ist in der bestehenden infizierten Kurve für den Fall SARS 2003 in Hongkong zu sehen? Daher kann eine minimale quadratische Anpassung des letzten Teils der Kurve vorgenommen werden

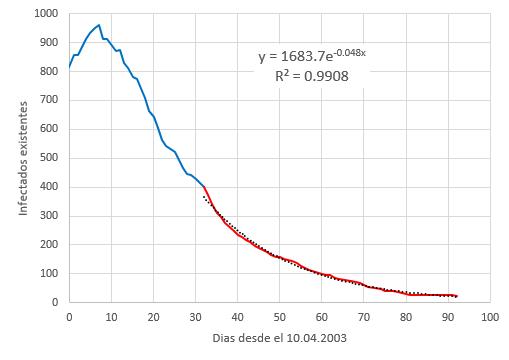
\\n\\nErhalten, dass der Faktor \gamma in der Größenordnung von 0,048 1 / Tag liegen muss. Dies entspricht einer durchschnittlichen Zeit von der Infektion bis zur Genesung von\\n\\n

$\tau=\displaystyle\frac{1}{\gamma}\sim 20.8,dias$

Wenn wir auch davon ausgehen, dass sich jede Person täglich in der Größenordnung von 30 Personen trifft, müsste der \beta -Faktor geschätzt werden, damit die vom Simulator erzeugte Kurve der von der WHO gemessenen Kurve ähnelt.

ID:(8203, 0)

Bild

>Top

Wenn die anfälligen, infizierten und 'erholten' (die heilen oder sterben) beobachtet werden, werden die typischen Kurven des SIR-Modells beobachtet:

ID:(9663, 0)

Bild

>Top

Wenn die Ansteckungs- und Entwicklungsparameter variiert werden, sind die Summen von:

• die Infizierten
• die erholten
• die Toten

Wie das folgende Bild zeigt:

ID:(9693, 0)

Bild

>Top

Wenn die Anzahl der Personen, die zu der Gruppe gehören, in der sich die Krankheit ausbreitet, sehr groß ist, überschreitet die Kurve tendenziell die gemessenen Daten:

ID:(9694, 0)

Bild

>Top

Wenn die Anzahl der Personen, die zu der Gruppe gehören, in der sich die Krankheit ausbreitet, sehr gering ist, überschreitet die Kurve tendenziell die gemessenen Daten:

ID:(9695, 0)

Bild

>Top

Wenn die Anzahl der Kontakte und die Infektionsrate zu groß sind, ist die Steigung zu groß (sehr steil):

ID:(9696, 0)

Bild

>Top

Wenn die Anzahl der Kontakte und die Infektionsrate zu gering sind, ist die Steigung zu gering (zu flach):

ID:(9697, 0)

Beschreibung

>Top

Die Verzögerungszeit ermöglicht es, die Kurve zu bewegen, indem sie ohne Verformung entlang der Zeitachse transportiert wird. Dies ist notwendig, da der Zeitpunkt, zu dem die Krankheit begonnen hat, unbekannt ist und für jede der Kurven einzeln existiert.\\n\\nJede Kurve bewegt sich einzeln in den Zeiten:\\n\\n• $t_{\rho}$ Zeit, wenn die erste Latente erscheint\\n• $t_{\beta}$ Zeitpunkt, zu dem die erste Infektion auftritt\\n• $t_{\gamma}$ Zeitpunkt, zu dem die erste Wiederherstellung angezeigt wird\\n• $t_{\delta}$ Zeitpunkt, zu dem der erste Tote erscheint\\n\\nIm Allgemeinen sollte es sein, dass die Zeiten so sind, dass\\n\\n

$t_{\rho} < t_{\beta} < t_{\gamma} < t_{\delta}$

gegeben die Reihenfolge der Ereignisse im Modell. Die Anpassung und Unsicherheit in den Daten kann jedoch zu unterschiedlichen Ordnungen führen, die darauf hinweisen, dass die Zeiten selbst nicht zuverlässig sind.

Es ist wichtig zu erkennen, dass der Offset sowohl positiv als auch negativ sein kann.

ID:(9702, 0)

Bild

>Top

Wenn die Verzögerungszeit jeder Kurve zu groß gewählt wird, wird die Kurve in Bezug auf die tatsächliche Entwicklung verzögert:

ID:(9698, 0)

Bild

>Top

Wenn die Verzögerungszeit jeder Kurve zu klein gewählt wird, bewegt sich die Kurve in Bezug auf die tatsächliche Entwicklung vorwärts:

ID:(9699, 0)

Bild

>Top

Wenn die Wiederherstellungsrate und die Latenzrate zu groß sind, wird die infizierte Kurve steiler, während sich die Wiederherstellungsrate abflacht. In diesem Sinne scheinen diese Faktoren beide Kurven zu drehen, indem sie den Winkel zwischen ihnen vergrößern (wenn sie wachsen) und verringern (wenn sie abnehmen).

ID:(9700, 0)

Bild

>Top

Wenn die Sterblichkeitsrate steigt, hat die entsprechende Kurve eine größere Beteiligung an der Bevölkerung, die nicht mehr infiziert und allgemein als 'wiederhergestellt' bezeichnet wird:

ID:(9701, 0)