Utilizador:
Caminho livre com gás
Conceito 
Quando uma partícula de um gás se move, ela interage com outras partículas. A forma mais simples dessa interação é através de colisões elásticas, o que significa que a partícula colide sem perder energia, mudando sua direção para impactar outra partícula.
Dentro desse processo, faz sentido definir o camino livre ($\bar{l}$), cujo valor dependerá de uma concentração ($c_n$).
ID:(1708, 0)
Caminho livre sem movimentação de vizinhos
Conceito
Quando uma partícula com um raio dado se move pelo espaço, ela efetivamente ocupa o espaço de um cilindro com o mesmo raio. Para que uma partícula colida com outra, a segunda deve ter parte de seu volume dentro desse cilindro. No caso mais extremo, a segunda partícula está localizada a uma distância de dois raios da primeira, de modo que a borda do cilindro toca um ponto na esfera mais próxima ao eixo do cilindro. O centro dessa esfera está a uma distância igual a um raio da superfície do cilindro:
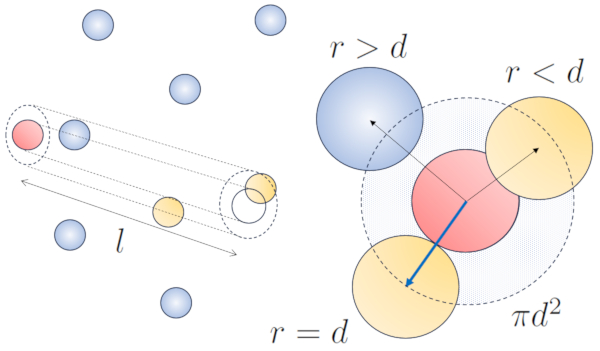
Portanto, a distância entre o eixo do cilindro e o centro de qualquer partícula é de dois raios, ou seja, um diâmetro. Em essência, pode-se imaginar que o volume ocupado literalmente pela partícula que se desloca pelo espaço é um cilindro com um comprimento igual ao caminho livre e um raio igual ao diâmetro da própria partícula.
ID:(1962, 0)
Caminho livre com circulação de vizinhos
Conceito
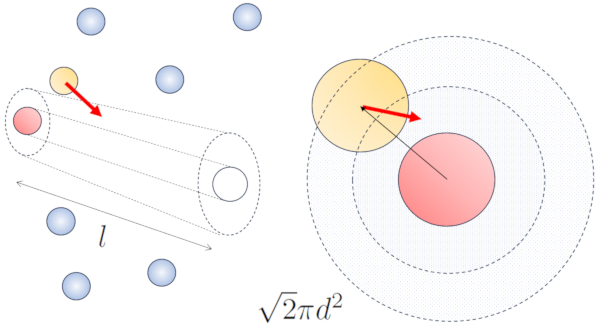
Quando partículas vizinhas estão em movimento, há uma maior probabilidade de colisão devido ao fato de que elas percorrem uma distância maior no mesmo intervalo de tempo. As componentes de velocidade, $v_x$, $v_y$ e $v_z$, flutuam em torno de valores médios $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ e $\sqrt{\langle v_z^2\rangle}$. Supondo que o sistema seja isotrópico, a média de cada componente será igual a $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Portanto, ao longo do eixo ao qual a partícula está se movendo, ela percorrerá uma distância
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
Ao mesmo tempo, as partículas que se movem perpendicularmente terão percorrido uma distância:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Portanto, a probabilidade de colisão aumenta em um fator de $\sqrt{2}$ em comparação com o caso em que as partículas não estão em movimento:
ID:(1963, 0)
Difusão de partículas
Conceito
Se houver uma diferença espacial em la concentração ($c_n$), ocorre um fenômeno conhecido como variação de concentração ($dc_n$). A probabilidade de as partículas chegarem a uma posição ao longo de um eixo ($z$) a partir de uma posição antes de uma distância de o camino livre ($\bar{l}$) é diferente da probabilidade a partir de uma posição após a mesma distância. Isso leva a mudanças em la concentração ($c_n$), um processo conhecido como difusão. A velocidade com que esse processo ocorre é a de la velocidade média de uma partícula ($\bar{v}$), e nele, $1/6$ das partículas participam em cada direção, pois há um total de 6 direções em um espaço tridimensional.
Dessa forma, é gerado la densidade de fluxo de partículas ($j$), que em termos de área corresponde a:
$j=\displaystyle\frac{1}{6}\bar{v}c(z-\bar{l}) - \displaystyle\frac{1}{6}\bar{v}c(z+\bar{l})=\displaystyle\frac{1}{6}\bar{v}[c(z-\bar{l})-c(z+\bar{l})]=-\displaystyle\frac{1}{6}\bar{v}2\bar{l}\displaystyle\frac{dc}{dz}$
As constantes que são fatorizadas ao calcular la densidade de fluxo de partículas ($j$) são resumidas em uma constante chamada la constante de difusão ($D$), que é igual a um terço do produto de o camino livre ($\bar{l}$) e la velocidade média de uma partícula ($\bar{v}$).
ID:(15143, 0)
Evaporação de água na camada
Conceito
O cálculo de la densidade de fluxo de partículas ($j$) com base em la variação de concentração ($dc_n$), variação de posição ($dz$) e la constante de difusão ($D$):
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
permite-nos determinar como a água evapora da camada freática. Para isso, os seguintes passos são necessários:
• Obtenha temperatura ambiente, umidade relativa, porosidade do solo e profundidade do lençol freático.
• Calcular a temperatura da água na superfície da camada freática.
• Calcular a concentração saturada de vapor de água acima da camada freática.
• Calcular a concentração de vapor de água acima do solo.
• Calcular o fluxo de vapor de água para o limite de fluxo estacionário.
ID:(15145, 0)
Modelo
Conceito
Variáveis
Parâmetros
Parâmetro selecionado
Cálculos
Equação
$ c_m \equiv\displaystyle\frac{ n }{ V }$
c_m = n / V
$ c_n = N_A c_m $
c_n = N_A * c_m
$ c_n =\displaystyle\frac{ \rho N_A }{ M_m }$
c_n = rho * N_A / M_m
$ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $
D = v * l /3
$ E =\displaystyle\frac{ f }{2} k_B T $
E = f * k_B * T /2
$ j =- D \displaystyle\frac{ dc_n }{ dz }$
j =- D * dc_n / dz
$ \vec{j} =- D \nabla c_n $
j =-D * nabla c_n
$ K =\displaystyle\frac{ m }{2} \bar{v} ^2$
K = m * v ^2/2
$ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$
l = 1/( d ^2 * pi * c )
$ m =\displaystyle\frac{ M_m }{ N_A }$
m = M_m / N_A
$ n =\displaystyle\frac{ M }{ M_m }$
n = M / M_m
$ n \equiv\displaystyle\frac{ N }{ N_A }$
n = N / N_A
$ \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }}$
v =sqrt( f * k_B * T / m )
$\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$
@DIFF( c_n, t, 1) = @DIFF( D * @DIFF( c_n , z , 1), z , 1)
$l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$
l = 1 / ( sqrt(2) * pi * d^2 * c_n )
ID:(15232, 0)
Concentração molar
Equação
La concentração molar ($c_m$) corresponde a número de moles ($n$) dividido por o volume ($V$) de um gás e é calculado da seguinte forma:
 $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
ID:(4878, 0)
Concentração molar
Equação
O número de moles ($n$) corresponde a o número de partículas ($N$) dividido por o número de Avogrado ($N_A$):
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
ID:(3748, 0)
Concentração de partículas e moles
Equação
Para converter a concentração molar $c_m$ em concentração de partículas $c$, basta multiplicar a primeira pelo número de Avogadro $N_A$ da seguinte maneira:
| $ c_n = N_A c_m $ |
ID:(10624, 0)
Número de moles com massa molar
Equação
O número de moles ($n$) é determinado dividindo la massa ($M$) de uma substância pelo seu la massa molar ($M_m$), que corresponde ao peso de um mol da substância.
Portanto, a seguinte relação pode ser estabelecida:
| $ n =\displaystyle\frac{ M }{ M_m }$ |
A massa molar é expressa em gramas por mol (g/mol).
ID:(4854, 0)
Concentração baseada na massa molar
Equação
Se dividirmos la densidade ($\rho$) por la massa molar ($M_m$), obteremos la concentração ($c_n$):
| $ c_n =\displaystyle\frac{ \rho N_A }{ M_m }$ |
Com la concentração ($c_n$) junto com la concentração molar ($c_m$) e o número de Avogrado ($N_A$), obtemos:
| $ c_n = N_A c_m $ |
Usando o número de moles ($n$) e o volume ($V$),
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
Com la massa ($M$) e la massa molar ($M_m$),
| $ n =\displaystyle\frac{ M }{ M_m }$ |
E com la densidade ($\rho$),
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Consequentemente,
$c_n=N_Ac_m=\displaystyle\frac{nN_A}{V}=\displaystyle\frac{N_A}{V}\displaystyle\frac{M}{M_m}=\displaystyle\frac{\rho N_A}{M_m}$
Portanto:
| $ c_n =\displaystyle\frac{ \rho N_A }{ M_m }$ |
ID:(10623, 0)
Caminho livre com concentração de partículas
Equação
O caminho médio livre pode ser estimado em termos do diâmetro de um cilindro imaginário que envolve uma partícula, em média, tendo uma colisão com outra partícula.
O raio do cilindro corresponde à distância máxima que duas partículas devem ter para colidir, o que equivale a duas vezes o raio da partícula, ou seja, o diâmetro de partícula ($d$). Como apenas uma colisão ocorre dentro deste cilindro, o número de partículas contidas nele deve ser igual a um. Isso significa que:
$l d^2\pi c_n= 1$
com la concentração ($c_n$), e resolvendo para o camino livre ($\bar{l}$), obtemos:
| $ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$ |
Isso representa o caminho médio livre.
ID:(4392, 0)
Estrada livre do meio para vizinhos em movimento
Equação
No caso sem movimento, a probabilidade é de o camino livre ($\bar{l}$), enquanto com movimento, as probabilidades são de o diâmetro de partícula ($d$) e la concentração ($c_n$), respectivamente.
No caso de movimento, a probabilidade aumenta em um fator de $\sqrt{2}$, o que significa que o caminho livre é
| $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)
Energia cinética da partícula
Equação
La energia cinética ($K$) combinado com ($$) e la velocidade média de uma partícula ($\bar{v}$) é igual a
| $ K =\displaystyle\frac{ m }{2} \bar{v} ^2$ |
Observação: Em um rigor mais estrito, a energia cinética depende da média da velocidade ao quadrado $\bar{v^2}$. No entanto, assume-se que isso é aproximadamente igual ao quadrado da média da velocidade:
$\bar{v^2}\sim\bar{v}^2$
ID:(4390, 0)
Massa de partículas
Equação
($$) pode ser estimado a partir de la massa molar ($M_m$) e o número de Avogrado ($N_A$) usando
| $ m =\displaystyle\frac{ M_m }{ N_A }$ |
ID:(4389, 0)
Energia baseada em graus de liberdade
Equação
A lei de Stefan-Boltzmann, inicialmente proposta por Josef Stefan [1] e posteriormente refinada por Ludwig Boltzmann [2], afirma que la energia de uma molécula ($E$) é proporcional a o graus de liberdade ($f$) multiplicado por la temperatura absoluta ($T$) com uma constante de proporcionalidade de la constante de Boltzmann ($k_B$):
| $ E =\displaystyle\frac{ f }{2} k_B T $ |
É importante destacar que la temperatura absoluta ($T$) deve ser expressa obrigatoriamente em graus Kelvin.
O número de graus de liberdade de uma partícula corresponde ao número de variáveis necessárias para descrever seu estado termodinâmico. Por exemplo, para uma partícula pontual, são necessárias apenas três coordenadas, resultando em três graus de liberdade. Se a partícula tiver forma e rigidez, serão necessários mais dois ângulos, resultando em um total de cinco graus de liberdade. Quando a partícula pode deformar-se ou vibrar em uma ou mais direções, esses modos adicionais também são considerados como graus de liberdade adicionais. No entanto, é importante notar que esses graus de liberdade adicionais existem apenas em altas temperaturas, quando a partícula possui energia suficiente para ativar tais vibrações.
[1] "Über die Beziehung zwischen der Wärmestrahlung und der Temperatur" (Sobre a Relação entre a Radiação de Calor e a Temperatura), Josef Stefan, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1879).
[2] "Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen" (Estudos Adicionais sobre o Equilíbrio Térmico entre Moléculas de Gás), Ludwig Boltzmann, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1884).
ID:(4387, 0)
Constante de difusão
Equação
A constante de difusão $D$ pode ser calculada a partir da velocidade média $\bar{v}$ e do caminho livre médio $\bar{l}$ das partículas.
| $ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $ |
É importante reconhecer que tanto o caminho médio livre quanto a velocidade média dependem da temperatura, e consequentemente, a constante de difusão também depende dela. Portanto, quando valores para a chamada constante são publicados, a temperatura à qual se refere sempre é especificada.
ID:(3186, 0)
Fick Lei em uma dimensão
Equação
Em 1855, Adolf Fick [1] formulou uma equação para o cálculo de la constante de difusão ($D$), resultando em la densidade de fluxo de partículas ($j$) devido a la variação de concentração ($dc_n$) ao longo de variação de posição ($dz$):
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
[1] "Über Diffusion" (Sobre Difusão), Adolf Fick, Annalen der Physik und Chemie, Volume 170, páginas 59-86 (1855)
ID:(4820, 0)
A lei de Fick em mais dimensões
Equação
La densidade de fluxo de partículas ($j$) em uma dimensão é calculado usando os valores la constante de difusão ($D$), la concentração ($c_n$) e la posição ao longo de um eixo ($z$), de acordo com a seguinte lei de Fick [1]:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Esta fórmula pode ser generalizada para mais de uma dimensão da seguinte forma:
| $ \vec{j} =- D \nabla c_n $ |
[1] "Über Diffusion" (Sobre Difusão), Adolf Fick, Annalen der Physik und Chemie, Volume 170, páginas 59-86 (1855)
ID:(4821, 0)
Equação de difusão de partículas
Equação
Se la constante de difusão ($D$) é igual a la densidade de fluxo de partículas ($j$) devido a la variação de concentração ($dc_n$) ao longo de variação de posição ($dz$), isso é regido pela lei de Fick [1]:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Portanto, para descrever a variação da concentração em o tempo ($t$), que corresponde à variação espacial da densidade de fluxo, obtemos a equação
| $\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$ |
[1] "Über Diffusion" (Sobre Difusão), Adolf Fick, Annalen der Physik und Chemie, Volume 170, páginas 59-86 (1855).
ID:(15144, 0)