Vapor de água no solo
Storyboard 
Variáveis
Cálculos
Cálculos
Equações
Usando a equa o de Clausius-Clapeyron para o gradiente de la pressão ($p$) em rela o a la temperatura absoluta ($T$), que depende de o calor latente ($L$) e la variação de volume na mudança de fase ($\Delta V$):
No caso da mudan a de fase de l quido para g s, podemos assumir que a mudan a de volume aproximadamente igual ao volume do vapor. Portanto, podemos empregar a equa o dos gases ideais com o número de moles ($n$), o volume ($V$), la constante de gás universal ($R_C$) e la pressão de vapor de água insaturada ($p_v$):
Uma vez que a equa o de Clausius-Clapeyron pode ser escrita como:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Onde o calor latente molar ($l_m$) ($l_m = L/n$) corresponde mudan a de entalpia durante a mudan a de fase h (a energia necess ria para formar gua), n s finalmente obtemos:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Se integramos esta equa o entre la pressão de vapor de água saturada ($p_s$) e a press o no ponto
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Se avaliarmos esta express o com os dados no ponto cr tico:
$p_{ref}=p_0e^{l_m/RT_0}$
N s finalmente temos:
Uma vez que o diferencial de energia interna ($dU$) depende de o diferencial de calor impreciso ($\delta Q$), la pressão ($p$), e la variação de volume ($\Delta V$) de acordo com a equa o:
e a express o da segunda lei da termodin mica com la temperatura absoluta ($T$) e la variação de entropia ($dS$) como:
podemos concluir que:
Se diferenciarmos a defini o de la entalpia ($H$), que depende de la energia interna ($U$), la pressão ($p$) e o volume ($V$), de acordo com:
obtemos:
$dH = dU + Vdp + pdV$
usando o diferencial de entalpia ($dH$), o diferencial de energia interna ($dU$), la variação de pressão ($dp$) e la variação de volume ($\Delta V$).
Ao diferenciar la energia interna ($U$) em rela o a la temperatura absoluta ($T$) e la entropia ($S$),
obtemos:
com o diferencial de energia interna ($dU$) e la variação de entropia ($dS$).
Portanto, conclu mos finalmente que:
La energia livre de Gibbs ($G$) em fun o de la entalpia ($H$), la entropia ($S$) e la temperatura absoluta ($T$) expresso da seguinte forma:
O valor de o diferencial de energia livre de Gibbs ($dG$) determinado usando o diferencial de entalpia ($dH$), la variação de temperatura ($dT$) e la variação de entropia ($dS$) atrav s da equa o:
$dG=dH-SdT-TdS$
Uma vez que o diferencial de entalpia ($dH$) est relacionado com o volume ($V$) e la variação de pressão ($dp$) da seguinte forma:
Segue-se que o diferencial de entalpia ($dH$), la variação de entropia ($dS$) e la variação de pressão ($dp$) est o interligados da seguinte maneira:
A rela o entre la umidade relativa ($RH$) com la concentração de moléculas de vapor de água ($c_v$) e ERROR:4952,0 expressa como:
e relacionando la pressão ($p$) com la concentração molar ($c_m$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), obtemos:
Isso se aplica press o de vapor de gua, onde:
$p_v = c_v R T$
e press o de vapor saturada de gua:
$p_s = c_s R T$
resultando na seguinte equa o:
Quando la pressão ($p$) se comporta como um g s ideal, cumprindo com o volume ($V$), o número de moles ($n$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), a equa o dos gases ideais:
e a defini o de la concentração molar ($c_m$):
levam seguinte rela o:
Com a lei de Clausius-Clapeyron, que depende de la variação de pressão ($dp$), la variação de temperatura ($dT$), o calor latente ($L$), la variação de volume na mudança de fase ($\Delta V$) e la temperatura absoluta ($T$), expressa como:
e a defini o de o calor latente molar ($l_m$), onde o calor latente ($L$) est relacionado a la massa molar ($M_m$) da seguinte forma:
e o variação do volume molar durante a mudança de fase ($\Delta v_m$), onde la variação de volume na mudança de fase ($\Delta V$) est relacionado a la massa molar ($M_m$) da seguinte forma:
obtemos:
Se o diferencial de energia livre de Gibbs ($dG$) constante, significa que, para la variação de pressão ($dp$) e la variação de temperatura ($dT$), os valores de la entropia ($S$) e o volume ($V$) na fase 1
$dG = -S_1dT+V_1dp$
e la entropia ($S$) e o volume ($V$) na fase 2
$dG = -S_2dT+V_2dp$
resultam em
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
A mudan a em la entropia ($S$) entre ambas as fases corresponde a o calor latente ($L$) dividido por la temperatura absoluta ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Assim, com a defini o de la variação de volume na mudança de fase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
obtemos
Exemplos
A fase gasosa, que no nosso caso corresponde ao vapor de gua, aquela em que os tomos podem se deslocar relativamente livremente.
Nesta fase, existe apenas uma intera o m nima que pode afetar o comportamento dos tomos sem confin -los significativamente.
A fase l quida, que no nosso caso corresponde gua, aquela em que os tomos podem mover-se relativamente livremente, mantendo a sua unidade e adaptando-se forma que os cont m.
Nesta fase, n o se observa nenhuma estrutura espec fica
A fase s lida, que no nosso caso corresponde ao gelo, aquela em que os tomos n o podem se deslocar relativamente, podendo apenas oscilar em torno de seu ponto de equil brio.
Nesta fase, pode-se observar uma estrutura que costuma ser cristalina e, portanto, regular.
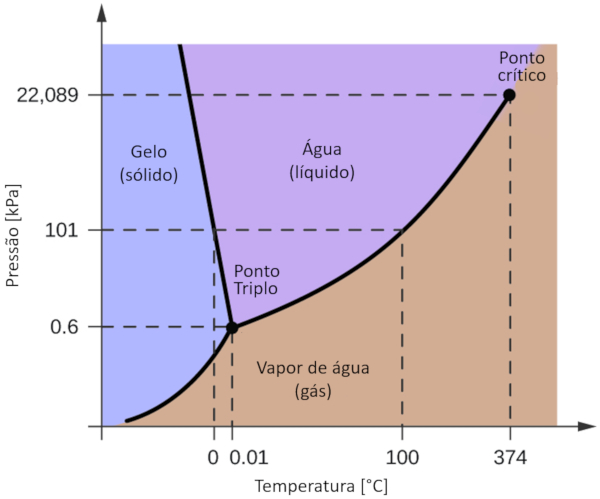
Um dos diagramas de fase mais relevantes para o nosso planeta o da gua. Este diagrama apresenta as tr s fases cl ssicas: s lida, l quida e gasosa, al m de v rias fases com diferentes estruturas cristalinas do gelo.
A diferen a significativa em rela o a outros materiais que, dentro de uma faixa de press o que varia de 611 Pa a 209,9 MPa, o estado s lido ocupa um volume maior do que o estado l quido. Essa caracter stica refletida no diagrama de fase como uma inclina o negativa ao longo da linha de separa o entre o estado s lido (gelo hexagonal) e o estado l quido ( gua).
Esse fen meno pode ser explicado pela equa o de Clausius-Clapeyron:
Neste caso, mostra uma varia o negativa no volume:
$\Delta v=v_{ gua}-v_{gelo}= 18,015,ml/mol-19,645,ml/mol=-1,63,ml/mol<0$
Essa propriedade leva a situa es em que, devido falta de espa o para expans o, a gua n o congela, preservando a vida contida nela. Por outro lado, a press o gerada pelo fato de o gelo ocupar mais volume um dos principais mecanismos de eros o na Terra.
A medi o do calor de vaporiza o realizada aquecendo uma amostra, o que a faz evaporar, enquanto simultaneamente se mede o calor entregue amostra. Em seguida, o vapor resfriado e condensado, e a massa que originalmente evaporou medida.
Dessa forma, podemos estimar a energia necess ria para vaporizar uma massa espec fica, o que corresponde a ERROR:5238,0 medido em joules por quilograma (J/kg) ou joules por mol (J/mol).
A fase gasosa da gua corresponde ao que conhecido como vapor de gua. Ela criada quando as mol culas de gua adquirem energia cin tica suficiente para escapar da fase l quida e come am a se mover pelo espa o acima do l quido. Periodicamente, as mol culas em estado gasoso colidem novamente com a superf cie l quida e s o capturadas, retornando ao estado l quido.
medida que o n mero de mol culas em estado gasoso aumenta, tamb m aumenta o n mero de mol culas que retornam ao estado l quido. Esse processo continua at que um equil brio seja alcan ado entre as mol culas que deixam o l quido e as que s o reabsorvidas. Nessa situa o, diz-se que o espa o acima do l quido est saturado.
O diferencial de energia interna ($dU$) sempre igual quantidade de o diferencial de calor impreciso ($\delta Q$) fornecida ao sistema (positiva) menos a quantidade de o diferencial de trabalho impreciso ($\delta W$) realizada pelo sistema (negativa):
Analogamente defini o do trabalho $dW$ na mec nica:
que definido em termos da for a $F$ e do deslocamento $dx$, na termodin mica, trabalhamos com a express o do trabalho em fun o da press o $p$ e da varia o de volume $dV$:
O diferencial de calor impreciso ($\delta Q$) igual a la temperatura absoluta ($T$) vezes la variação de entropia ($dS$):
A depend ncia de o diferencial de energia interna ($dU$) de la pressão ($p$) e la variação de volume ($\Delta V$), al m de la temperatura absoluta ($T$) e la variação de entropia ($dS$) , dado por:
La entalpia ($H$) definido como a soma de la energia interna ($U$) e a energia de forma o. Esta ltima corresponde ao trabalho realizado na forma o, que igual a $pV$ com la pressão ($p$) e o volume ($V$). Portanto, temos:
A depend ncia de o diferencial de entalpia ($dH$) de la temperatura absoluta ($T$) e la variação de entropia ($dS$), al m de o volume ($V$) e la variação de pressão ($dp$) , dado por:
A depend ncia de ERROR:5402 de la entropia ($S$) e la variação de temperatura ($dT$), al m de o volume ($V$) e la variação de pressão ($dp$) , dado por:
A lei Clausius-Clapeyron estabelece uma rela o entre la variação de pressão ($dp$) e la variação de temperatura ($dT$) com o calor latente ($L$), la temperatura absoluta ($T$) e ERROR:5239 < /var> da seguinte maneira:
A equa o de Clausius-Clapeyron estabelece uma rela o entre la variação de pressão ($dp$) e la variação de temperatura ($dT$) com la temperatura absoluta ($T$), o calor latente molar ($l_m$) e ERROR:9868 < /var> da seguinte maneira:
Quando la variação de volume na mudança de fase ($\Delta V$) muda de fase de um l quido para um g s, pode ser expresso como:
$\Delta V = V_{\text{g s}} - V_{\text{l quido}}$
Dado que o volume do g s significativamente maior do que o do l quido,
$V_{\text{g s}} \gg V_{\text{l quido}}$
podemos aproximar:
$\Delta V \approx V_{\text{g s}}$
Como o vapor de gua se comporta de maneira semelhante a um g s ideal, podemos afirmar que com os valores de la constante de gás universal ($R_C$), o número de moles ($n$), la temperatura absoluta ($T$) e la pressão de vapor de água insaturada ($p_v$):
portanto, la variação de volume na mudança de fase ($\Delta V$) :
$\Delta V = \displaystyle\frac{nRT}{p_v}$
La pressão de vapor de água saturada ($p_s$) pode ser calculado usando la pressão de referência ($p_{ref}$), la constante de gás universal ($R_C$), la temperatura absoluta ($T$) e o calor latente molar ($l_m$) de acordo com o seguinte f rmula:
La relation entre la concentração de moléculas de vapor de água ($c_v$) et ERROR:4952,0 est appel e la umidade relativa ($RH$). En d'autres termes, lorsque l'humidit relative atteint 100 %, la concentration existante est gale la concentration satur e.
La pressão ($p$) pode ser calculado a partir de la concentração molar ($c_m$) utilizando la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) da seguinte maneira:
La umidade relativa ($RH$) pode ser expresso em termos de la pressão de vapor de água insaturada ($p_v$) e la pressão de vapor de água saturada ($p_s$) como segue:
ID:(377, 0)