Diffusion de vapeur d'eau dans le sol
Storyboard 
Variables
Calculs
Calculs
Équations
Le nombre de taupes ($n$) correspond le nombre de particules ($N$) divis par le numéro d'Avogadro ($N_A$) :
Si nous multiplions la fois le num rateur et le d nominateur par a masse molaire ($m$), nous obtenons :
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
Donc, c'est :
Avec a concentration de particules ($c_n$) comme le nombre de particules ($N$) et le volume ($V$), nous obtenons :
Avec a masse molaire ($m$) et a masse ($M$),
Comme a densité ($\rho$) est
nous obtenons
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Ainsi,
Exemples
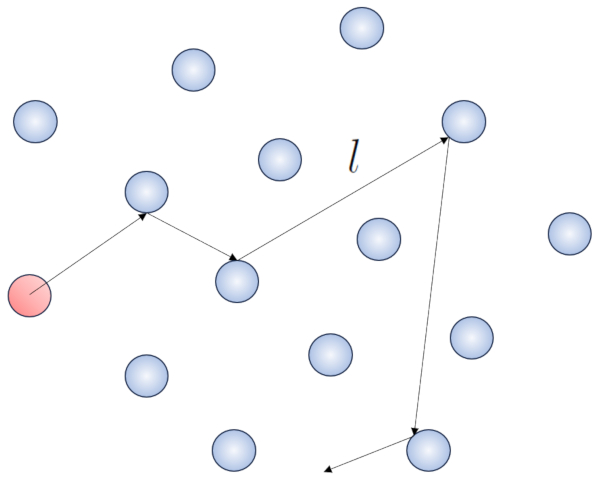
Quand une particule d'un gaz se d place, elle interagit avec les autres particules. La forme la plus simple de cette interaction se produit travers des collisions lastiques, ce qui signifie que la particule entre en collision sans perdre d' nergie, changeant sa direction pour ensuite entrer en collision avec une autre particule.
Dans ce processus, il est judicieux de d finir le route libre ($\bar{l}$), dont la valeur d pendra de une concentration de particules ($c_n$).
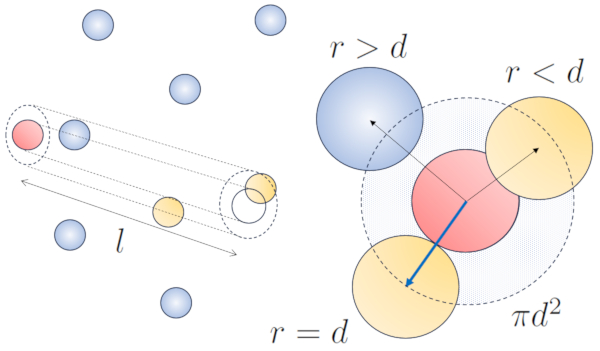
Lorsqu'une particule dot e d'un rayon donn se d place dans l'espace, elle occupe effectivement l'espace d'un cylindre avec le m me rayon. Pour qu'une particule entre en collision avec une autre, la seconde doit avoir une partie de son volume l'int rieur de ce cylindre. Dans le cas le plus extr me, la deuxi me particule se trouve une distance de deux rayons de la premi re, de sorte que le bord du cylindre touche un point de la sph re le plus proche de l'axe du cylindre. Le centre de cette sph re est situ une distance gale un rayon de la surface du cylindre :
Par cons quent, la distance entre l'axe du cylindre et le centre de n'importe quelle particule est de deux rayons, autrement dit, un diam tre. En essence, on peut imaginer que le volume litt ralement occup par la particule se d pla ant dans l'espace est un cylindre ayant une longueur gale au libre parcours et un rayon gal au diam tre de la particule elle-m me.
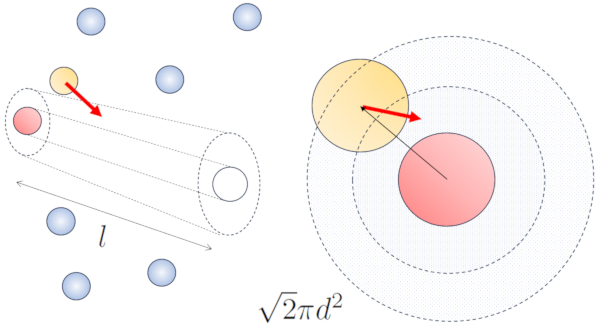
Lorsque des particules voisines sont en mouvement, il existe une probabilit plus lev e de collision en raison du fait qu'elles parcourent une plus grande distance en m me temps. Les composantes de vitesse, $v_x$, $v_y$ et $v_z$, fluctuent autour de valeurs moyennes $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ et $\sqrt{\langle v_z^2\rangle}$. En supposant que le syst me soit isotrope, la moyenne de chaque composante sera gale $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Par cons quent, le long de l'axe le long duquel la particule se d place, elle parcourra une distance
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
En m me temps, les particules se d pla ant perpendiculairement auront parcouru une distance :
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Ainsi, la probabilit de collision augmente d'un facteur de $\sqrt{2}$ par rapport au cas o les particules ne sont pas en mouvement :
S'il existe une diff rence spatiale dans a concentration de particules ($c_n$), un ph nom ne connu sous le nom de ERROR:6597,0 se produit. La probabilit que les particules atteignent une positionner le long d'un axe ($z$) partir d'une position avant une distance de le route libre ($\bar{l}$) est diff rente de la probabilit partir d'une position apr s la m me distance. Cela conduit des changements dans a concentration de particules ($c_n$), un processus connu sous le nom de diffusion. La vitesse laquelle ce processus se produit est celle de a vitesse moyenne d'une particule ($\bar{v}$), et en elle, $1/6$ des particules participent dans chaque direction, car il y a un total de 6 directions dans un espace tridimensionnel.
De cette mani re, a densité de flux de particules ($j$) est g n r , qui en termes de superficie correspond :
$j=\displaystyle\frac{1}{6}\bar{v}c(z-\bar{l}) - \displaystyle\frac{1}{6}\bar{v}c(z+\bar{l})=\displaystyle\frac{1}{6}\bar{v}[c(z-\bar{l})-c(z+\bar{l})]=-\displaystyle\frac{1}{6}\bar{v}2\bar{l}\displaystyle\frac{dc}{dz}$
Les constantes qui sont factoris es lors du calcul de a densité de flux de particules ($j$) sont r sum es en une constante appel e a constante de diffusion ($D$), qui est gale au tiers du produit de le route libre ($\bar{l}$) et a vitesse moyenne d'une particule ($\bar{v}$).
Le calcul de a densité de flux de particules ($j$) en fonction de a variation des concentrations ($dc_n$), ERROR:10192,0 et a constante de diffusion ($D$) :
nous permet de d terminer comment l'eau s' vapore de la nappe phr atique. Pour ce faire, les tapes suivantes sont n cessaires :
• Obtenez la temp rature ambiante, lhumidit relative, la porosit du sol et la profondeur de la nappe phr atique.
• Calculer la temp rature de l'eau la surface de la nappe phr atique.
• Calculer la concentration satur e de vapeur d'eau au-dessus de la nappe phr atique.
• Calculer la concentration de vapeur d'eau au-dessus du sol.
• Calculer le flux de vapeur d'eau pour la limite de flux stationnaire.
A concentration molaire ($c_m$) correspond ERROR:9339,0 divis par le volume ($V$) d'un gaz et est calcul comme suit :
Le nombre de taupes ($n$) correspond le nombre de particules ($N$) divis par le numéro d'Avogadro ($N_A$) :
le numéro d'Avogadro ($N_A$) est une constante universelle de valeur 6.028E+23 1/mol ; elle nest donc pas incluse parmi les variables utilis es dans le calcul.
Pour convertir a concentration molaire ($c_m$) en a concentration de particules ($c_n$), il suffit de multiplier la premi re par le numéro d'Avogadro ($N_A$), comme suit :
Le nombre de taupes ($n$) est d termin en divisant a masse ($M$) d'une substance par son a masse molaire ($M_m$), ce qui correspond au poids d'une mole de la substance.
Par cons quent, la relation suivante peut tre tablie :
La masse molaire est exprim e en grammes par mole (g/mol).
Si nous divisons a densité ($\rho$) par a masse molaire ($m$), nous obtiendrons a concentration de particules ($c_n$) :
La longueur libre moyenne peut tre estim e en fonction du diam tre d'un cylindre imaginaire entourant une particule, en moyenne ayant une collision avec une autre particule.
Le rayon du cylindre correspond la distance maximale que deux particules doivent avoir pour entrer en collision, ce qui quivaut deux fois le rayon de la particule, c'est- -dire le diamètre des particules ($d$). Comme seule une collision se produit l'int rieur de ce cylindre, le nombre de particules qu'il contient doit tre gal un. Cela signifie que :
$l d^2\pi c_n= 1$
avec a concentration de particules ($c_n$), et en r solvant pour le route libre ($\bar{l}$), nous obtenons :
Cela repr sente la longueur libre moyenne.
Dans le cas sans mouvement, la probabilit est de le route libre ($\bar{l}$), tandis qu'avec le mouvement, les probabilit s sont de le diamètre des particules ($d$) et a concentration de particules ($c_n$), respectivement.
Dans le cas du mouvement, la probabilit augmente d'un facteur de $\sqrt{2}$, ce qui signifie que le chemin libre est
A énergie cinétique ($K$) en combinaison avec a masse molaire ($m$) et a vitesse moyenne d'une particule ($\bar{v}$) quivaut
Remarque : Dans un strict respect des r gles, l' nergie cin tique d pend de la moyenne de la vitesse au carr $\bar{v^2}$. Cependant, on suppose que cela est approximativement gal au carr de la moyenne de la vitesse :
$\bar{v^2}\sim\bar{v}^2$
A masse molaire ($m$) peut tre estim partir de a masse molaire ($M_m$) et le numéro d'Avogadro ($N_A$) en utilisant
La loi de Stefan-Boltzmann, initialement propos e par Josef Stefan [1] et ensuite affin e par Ludwig Boltzmann [2], tablit que a énergie d'une molécule ($E$) est proportionnelle le degrés de liberté ($f$) multipli e par a température absolue ($T$) avec une constante de proportionnalit de a constante de Boltzmann ($k_B$) :
Il est important de noter que a température absolue ($T$) doit tre exprim e en degr s Kelvin.
Le nombre de degr s de libert d'une particule correspond au nombre de variables n cessaires pour d crire son tat thermodynamique. Par exemple, pour une particule ponctuelle, seules trois coordonn es sont n cessaires, ce qui donne lieu trois degr s de libert . Si la particule a une forme et une rigidit , deux angles suppl mentaires sont n cessaires, ce qui entra ne un total de cinq degr s de libert . Lorsque la particule peut se d former ou vibrer dans une ou plusieurs directions, ces modes suppl mentaires sont galement consid r s comme des degr s de libert suppl mentaires. Cependant, il est important de noter que ces degr s de libert suppl mentaires n'existent qu' des temp ratures lev es, lorsque la particule a suffisamment d' nergie pour activer de telles vibrations.
[1] " ber die Beziehung zwischen der W rmestrahlung und der Temperatur" (Sur la Relation entre le Rayonnement Thermique et la Temp rature), Josef Stefan, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1879).
[2] "Weitere Studien ber das W rmegleichgewicht unter Gasmolek len" ( tudes Suppl mentaires sur l' quilibre Thermique entre les Mol cules de Gaz), Ludwig Boltzmann, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1884).
La constante de diffusion $D$ peut tre calcul e partir de la vitesse moyenne $\bar{v}$ et du libre parcours moyen $\bar{l}$ des particules.
Il est important de reconna tre que tant le libre parcours moyen que la vitesse moyenne d pendent de la temp rature, et par cons quent, la constante de diffusion en d pend galement. C'est pourquoi, lors de la publication de valeurs pour la pr tendue constante, la temp rature laquelle elle s'applique est toujours sp cifi e.
En 1855, Adolf Fick [1] a formul une quation pour le calcul de a constante de diffusion ($D$), ce qui conduit a densité de flux de particules ($j$) en raison de a variation des concentrations ($dc_n$) le long de ERROR:10192,0:
[1] " ber Diffusion" (Sur la diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855)
A densité de flux de particules ($j$) en une dimension est calcul en utilisant les valeurs a constante de diffusion ($D$), a concentration de particules ($c_n$) et a positionner le long d'un axe ($z$), conform ment la loi de Fick [1] suivante:
Cette formule peut tre g n ralis e pour plus d'une dimension comme suit :
[1] " ber Diffusion" (Sur la diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855)
Si a constante de diffusion ($D$) est gal a densité de flux de particules ($j$) en raison de a variation des concentrations ($dc_n$) le long de ERROR:10192,0, cela est r gi par la loi de Fick [1] :
Par cons quent, pour d crire la variation de la concentration le temps ($t$), correspondant la variation spatiale de la densit de flux, nous obtenons l' quation suivante :
[1] " ber Diffusion" (Sur la Diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855).
ID:(376, 0)