Usuario:
Difusión
Storyboard 
Cuando existen variaciones en la concentración de un gas ocurre el fenómeno de difusión que tiende a reducir las variaciones. Este ocurre simplemente porque es mas probable que una molécula se desplace de una zona de mayor concentración a una de menor que a la inversa simplemente por el numero de moléculas existentes.
ID:(1311, 0)
Presión
Concepto
La presión es el resultado de las múltiples colisiones de las partículas del gas con las paredes del recipiente. Cada colisión contribuye a la presión total ejercida por el gas. Cuanto más rápido se muevan las partículas y cuantas más colisiones ocurran en un período de tiempo determinado, mayor será la presión.
ID:(9599, 0)
Volumen
Concepto
El volumen es una propiedad fundamental de un gas y se puede entender como el espacio tridimensional que el gas ocupa en un recipiente.
ID:(9601, 0)
Los moles
Concepto
Al emplear el concepto de mol, podemos establecer una relación directa entre la cantidad de sustancia de un gas y la cantidad de partículas de el número de partículas ($N$) presentes en él. Esto simplifica los cálculos y permite una conexión más intuitiva entre la cantidad de gas y las propiedades que lo describen, tales como la presión ($p$), el volumen ($V$) y la temperatura absoluta ($T$).
La constante el número de Avogadro ($N_A$), que es aproximadamente igual a $6,02\times 10^{23}$, representa una constante fundamental en la química y se utiliza para realizar conversiones entre la escala macroscópica y la escala microscópica de los átomos y las moléculas.
El valor de el número de Moles ($n$) se puede calcular a partir de el número de partículas ($N$) y la masa ($M$). En el primer caso, se obtiene dividiendo por ERROR:5403 utilizando la fórmula:
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
Mientras que en el segundo caso, se utiliza la masa molar ($M_m$) con la fórmula:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
ID:(9600, 0)
Ley de Charles
Hipótesis
En 1780 Jacques Charles descubrió que a y en un el Volumen
| $\displaystyle\frac{ V }{ T }= cte $ |
En este caso si la entonces el .
ID:(9518, 0)
Relación temperatura vs presión
Descripción
En un gas, cuando se mantienen constantes el volumen ($V$) y el número de partículas ($N$), se observa que la presión ($p$) y la temperatura absoluta ($T$) varían de manera proporcional. Cuando la temperatura absoluta ($T$) disminuye, la presión ($p$) también disminuye, y viceversa,
$p \propto T$
como se ilustra en el siguiente gráfico:
La ley de Gay-Lussac [1] establece que cuando ERROR:5226,0 y el número de partículas ($N$) se mantienen constantes, la presión ($p$) y la temperatura absoluta ($T$) son directamente proporcionales.
Esto se expresa con la constante de la ley de Gay Lussac ($C_g$) de la siguiente manera:
| $\displaystyle\frac{ p }{ T } = C_g$ |
[1] "Mémoire sur la combinaison des substances gazeuses les unes avec les autres" (Memoria sobre la combinación de sustancias gaseosas entre sí), Joseph Louis Gay-Lussac, Annales scientifiques de l'É.N.S. 3e série, tome 3 (1886)
ID:(9530, 0)
Ley de Gay Lussac
Hipótesis
Alrededor de 1808 Joseph Louis Gay-Lussac, en conjunto con otros cientificos, descubrió que a y en un la Presión
| $\displaystyle\frac{p}{T}=cte$ |
En este caso si la entonces la .
ID:(9519, 0)
Relación temperatura vs volumen
Descripción
En un gas, si se mantiene constante la presión ($p$) y el número de partículas ($N$), se observa que el volumen ($V$) y la temperatura absoluta ($T$) varían de forma proporcional. Cuando el volumen ($V$) disminuye, la temperatura absoluta ($T$) también disminuye, y viceversa,
$V \propto T$
como se ilustra en el siguiente gráfico:
La ley de Charles [1] establece que, manteniendo la presión ($p$) y el número de partículas ($N$) constantes, el volumen ($V$) y la temperatura absoluta ($T$) son directamente proporcionales.
Esto se puede expresar con la constante de la ley de Charles ($C_c$) de la siguiente manera:
| $\displaystyle\frac{ V }{ T } = C_c$ |
[1] "Sur la dilatación de los gases y vapores" (Sobre la expansión de gases y vapores), Jacques Charles, Academia de Ciencias de Francia (1787)
ID:(9529, 0)
Ley de Boyle
Hipótesis
En 1662 Robert Boyle descubrió que a y en un la Presión
| $ p V = cte$ |
En este caso si el entonces la .
ID:(9520, 0)
Relación volumen y presión
Descripción
En un gas, si se mantienen la temperatura absoluta ($T$) y el número de partículas ($N$) constantes, se observa que el volumen ($V$) y la presión ($p$) varían de forma inversamente proporcional. Cada vez que se reduce el volumen ($V$), se observa que la presión ($p$) aumenta y viceversa,
$p \propto \displaystyle\frac{1}{V}$
como se ilustra en el siguiente gráfico:
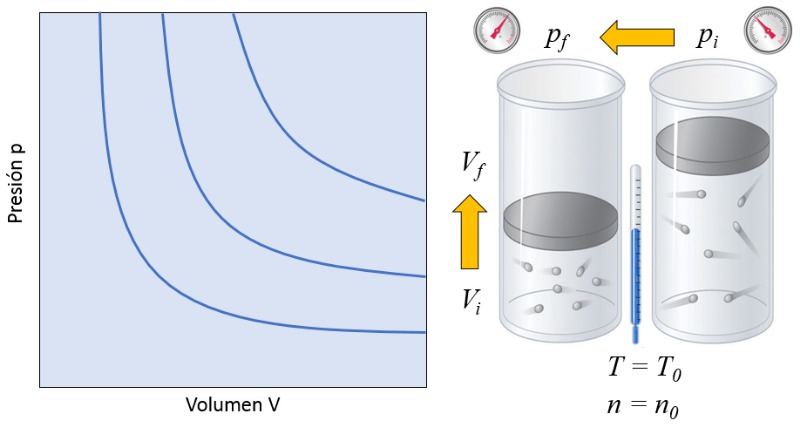
La relación entre el número de partículas ($N$) y la temperatura absoluta ($T$) es que su producto es igual a una constante de la ley de Boyle ($C_b$), lo que corresponde a la ley de Boyle [1], en honor a su descubridor Robert Boyle:
| $ p V = C_b $ |
Algunas veces se habla de la ley Boyle-Mariotte recordando al físico frances Edme Mariotte que descubrio en 1676 la misma ley en forma independiente. [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Nuevos experimentos físico-mecánicos, tocando el resorte del aire y sus efectos), Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).
ID:(9531, 0)
Ley de Avogadro
Hipótesis
En 1811 Amedeo Avogadro postula que a y en un el Numero de moles
| $\displaystyle\frac{n}{V}=cte$ |
En este caso si el entonces el .
ID:(9521, 0)
Relación moles y volumen
Descripción
En un gas, cuando se mantienen constantes la presión ($p$) y la temperatura absoluta ($T$), se observa una variación proporcional entre el volumen ($V$) y el número de moles ($n$). Cada vez que el volumen ($V$) aumenta, se nota un aumento correspondiente en el número de moles ($n$), y viceversa,
$n \propto V$
como se ilustra en el siguiente gráfico:
La Ley de Avogadro [1] establece que el volumen ($V$) y el número de moles ($n$) son directamente proporcionales cuando se mantienen constantes la presión ($p$) y la temperatura absoluta ($T$).
Esta relación se puede expresar de la siguiente manera, utilizando la constante del principio de Avogadro ($C_a$):
| $\displaystyle\frac{ n }{ V } = C_a $ |
[1] "Essai d'une manière de déterminer les masses relatives des molécules élémentaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons" (Ensayo sobre un método para determinar las masas relativas de las moléculas elementales de las sustancias y las proporciones en las que intervienen en sus combinaciones), Amedeo Avogadro, Journal de Physique, 73, 58-76 (1811)
ID:(9532, 0)
Integrando las leyes de los gases
Descripción
Las tres leyes de los gases que relacionan la presión ($p$), el volumen ($V$) y la temperatura absoluta ($T$) son:
• La ley de Boyle, que establece que a temperatura constante, el producto de la presión y el volumen de un gas es constante:
| $ p V = C_b $ |
• La ley de Charles, que establece que a presión constante, el volumen de un gas es directamente proporcional a su temperatura absoluta:
| $\displaystyle\frac{ V }{ T } = C_c$ |
• La ley de Gay-Lussac, que establece que a volumen constante, la presión de un gas es directamente proporcional a su temperatura absoluta:
| $\displaystyle\frac{ p }{ T } = C_g$ |
Estas leyes se pueden representar gráficamente como se muestra en la siguiente imagen:
Diagram presión, volumen, temperatura de un gas ideal (http://hyperphysics.phy-astr.gsu.edu)
En 1834, Émile Clapeyron [1] reconoció que la presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) se relacionan mediante la ley de Boyle, la ley de Charles, la ley de Gay-Lussac y la ley de Avogadro. Estas leyes pueden ser expresadas de manera más general como:
$\displaystyle\frac{pV}{nT} = \text{cte}$
Esta relación general establece que el producto de la presión y el volumen dividido por el número de moles y la temperatura se mantiene constante:
| $ p V = n R_C T $ |
En esta ecuación, la constante universal de los gases ($R_C$) asume el valor de 8.314 J/K·mol.[1] "Mémoire sur la puissance motrice de la chaleur" (Memoria sobre el poder motriz del calor), Émile Clapeyron, Journal de l'École Polytechnique, 1834.
ID:(9525, 0)