Diffusion
Storyboard 
When there are variations in the concentration of a gas, the diffusion phenomenon tends to reduce the variations. This occurs simply because a molecule is more likely to move from an area of greater concentration to one of less than in reverse simply by the number of existing molecules.
ID:(1311, 0)
Temperature vs. pressure relationship
Equation 
In a gas, when the volume ($V$) and the number of particles ($N$) are held constant, it is observed that the pressure ($p$) and the absolute temperature ($T$) vary proportionally. When the absolute temperature ($T$) decreases, the pressure ($p$) also decreases, and vice versa,
$p \propto T$
as shown in the following graph:

Gay-Lussac's law [1] states that when the volume ($V$) and the number of particles ($N$) are held constant, the pressure ($p$) and the absolute temperature ($T$) are directly proportional.
This is expressed with the gay Lussac's law constant ($C_g$) as follows:
| $\displaystyle\frac{ p }{ T } = C_g$ |
![]() [1] "Memoir on the Combination of Gaseous Substances with Each Other," Joseph Louis Gay-Lussac, Annales scientifiques de l'É.N.S. 3rd series, tome 3 (1886)
[1] "Memoir on the Combination of Gaseous Substances with Each Other," Joseph Louis Gay-Lussac, Annales scientifiques de l'É.N.S. 3rd series, tome 3 (1886)
ID:(9530, 0)
Temperature vs volume relationship
Script 
In a gas, if the pressure ($p$) and the number of particles ($N$) are held constant, it is observed that the volume ($V$) and the absolute temperature ($T$) vary in proportion. When the volume ($V$) decreases, the absolute temperature ($T$) also decreases, and vice versa,
$V \propto T$
as shown in the following graph:

Charles's law [1] states that, with the pressure ($p$) and the number of particles ($N$) held constant, the volume ($V$) and the absolute temperature ($T$) are directly proportional.
This can be expressed with the charles law constant ($C_c$) as follows:
| $\displaystyle\frac{ V }{ T } = C_c$ |
![]() [1] "Sur la dilatación de los gases y vapores" (On the Expansion of Gases and Vapors), Jacques Charles, French Academy of Sciences (1787)
[1] "Sur la dilatación de los gases y vapores" (On the Expansion of Gases and Vapors), Jacques Charles, French Academy of Sciences (1787)
ID:(9529, 0)
Volume vs. pressure relationship
Variable 
In a gas, if both the absolute temperature ($T$) and the number of particles ($N$) are kept constant, it is observed that the volume ($V$) and the pressure ($p$) vary inversely. Whenever the volume ($V$) is reduced, the pressure ($p$) increases, and vice versa,
$p \propto \displaystyle\frac{1}{V}$
as illustrated in the following graph:
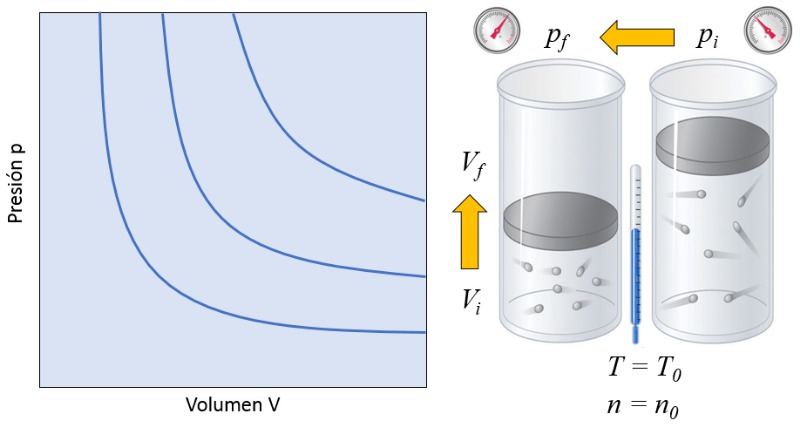
The relationship between the number of particles ($N$) and the absolute temperature ($T$) is that their product is equal to a boyle's law constant ($C_b$), which corresponds to Boyle's law [1], named after its discoverer Robert Boyle:
| $ p V = C_b $ |
Sometimes we talk about the Boyle-Mariotte law, remembering the French physicist Edme Mariotte who discovered the same law independently in 1676.
![]() [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects," Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).
[1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects," Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).
ID:(9531, 0)
Moles and volume ratio
Audio 
In a gas, when the pressure ($p$) and the absolute temperature ($T$) are held constant, a proportional relationship is observed between the volume ($V$) and the number of moles ($n$). Each time the volume ($V$) increases, it is observed that the number of moles ($n$) also increases, and vice versa,
$n \propto V$
as shown in the following graph:

Avogadro's Law [1] states that the volume ($V$) and the number of moles ($n$) are directly proportional when the pressure ($p$) and the absolute temperature ($T$) are held constant.
This relationship can be expressed as follows, using the constant of Avogadro's principle ($C_a$):
| $\displaystyle\frac{ n }{ V } = C_a $ |
![]() [1] "Essay on a Method of Determining the Relative Masses of the Elementary Molecules of Bodies and the Proportions in Which They Enter into These Compounds," Amedeo Avogadro, Journal de Physique, 73, 58-76 (1811).
[1] "Essay on a Method of Determining the Relative Masses of the Elementary Molecules of Bodies and the Proportions in Which They Enter into These Compounds," Amedeo Avogadro, Journal de Physique, 73, 58-76 (1811).
ID:(9532, 0)
Integrating the gas laws
Video 
The three gas laws that relate to the pressure ($p$), the volume ($V$), and the absolute temperature ($T$) are:
• Boyle's Law, which states that at constant temperature, the product of the pressure and the volume of a gas is constant:
| $ p V = C_b $ |
• Charles's Law, which states that at constant pressure, the volume of a gas is directly proportional to its absolute temperature:
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Gay-Lussac's Law, which states that at constant volume, the pressure of a gas is directly proportional to its absolute temperature:
| $\displaystyle\frac{ p }{ T } = C_g$ |
These laws can be graphically represented as shown in the following image:

In 1834, Émile Clapeyron [1] recognized that the pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related by Boyle's law, Charles's law, Gay-Lussac's law, and Avogadro's law. These laws can be expressed more generally as:
$\displaystyle\frac{pV}{nT} = \text{constant}$
This general relationship states that the product of pressure and volume divided by the number of moles and the temperature remains constant:
| $ p V = n R_C T $ |
In this equation, the universal gas constant ($R_C$) assumes the value of 8.314 J/K·mol.
[1] "Mémoire sur la puissance motrice de la chaleur" (Memoir on the Motive Power of Heat), Émile Clapeyron, Journal de l'École Polytechnique, 1834.
ID:(9525, 0)
