Druyd:Knowledge

Condición de Equilibrio y Temperatura

Storyboard

Para modelar sistemas con la mecánica estadística, es necesario examinar cómo los parámetros que describen el sistema macroscópico pueden afectar a los ensambles estadísticos. En el caso de partículas, el parámetro de temperatura se establece como un indicador de si los sistemas están en equilibrio, manteniendo sus energías a un nivel constante.

>Modelo

ID:(436, 0)

Un Sistema en contacto con un reservorio

Definición

ID:(11541, 0)

Comparando las curvas de número de estados

Imagen

ID:(11542, 0)

Formación de un máximo

Nota

ID:(11543, 0)

Condición de Equilibrio y Temperatura

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$\beta$

beta

Beta del reservorio

1/J

$\beta$

beta

Beta del sistema

1/J

$k_B$

k_B

Constante de Boltzmann

J/K

$E_2$

E_2

Energía del reservorio

$E$

Energía del sistema

$C$

Factor de normalización

$\Omega_E$

Omega_E

Numero de estados del reservorio con energía $E'$

$\Omega(E_0-E)$

Omega_E_0E

Numero de estados del reservorio con energía $E_0-E$

$\Omega_E$

Omega_E

Numero de estados del sistema con la energía $E$

$P_E$

P_E

Probabilidad del sistema de tener una energía $E$

$T_2$

T_2

Temperatura del reservorio

$T$

Temperatura del sistema

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$P(E)=C\Omega(E)\Omega(E_0-E)$

P(E)=C\Omega(E)\Omega(E_0-E)

(ID 3434)

$\beta(E)\equiv\displaystyle\frac{\partial\ln\Omega}{\partial E}$

\beta(E)\equiv\displaystyle\frac{\partial\ln\Omega}{\partial E}

(ID 3435)

$\beta(E)=\beta(E_h)$

\beta(E)=\beta(E_h)

(ID 3436)

$ k_B T \equiv\displaystyle\frac{1}{ \beta }$

k_B * T = 1/ beta

(ID 3437)

$ T = T_h $

T = T_h

(ID 3438)

$\displaystyle\frac{\partial\ln\Omega}{\partial E}-\displaystyle\frac{\partial\ln\Omega_h}{\partial E_h}=0$

d ln Omega/dE-d ln Omega/dE_h =0

(ID 3441)

$\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega_h}\displaystyle\frac{\partial\Omega_h}{\partial E_h}=0$

\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega_h}\displaystyle\frac{\partial\Omega_h}{\partial E_h}=0

(ID 4806)

Ejemplos

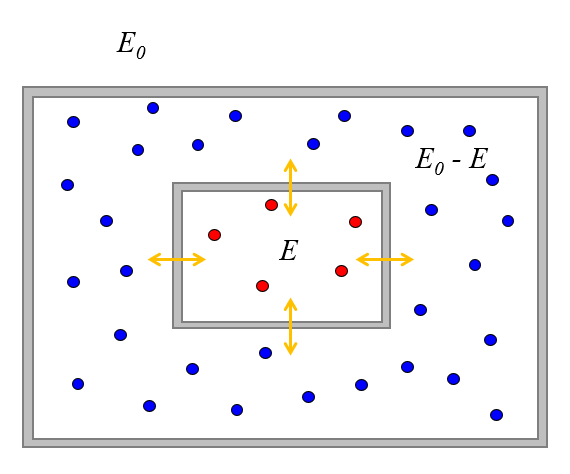
Un Sistema en contacto con un reservorio

Puedemos estudiar lo que ocurre cuando ponemos dos sistemas de part culas en contacto de manera que puedan intercambiar energ a pero no part culas.

Supongamos adem s que el sistema est aislado del entorno, por lo que tiene una energ a total $E_0$.

Supongamos que inicialmente el primer sistema tiene una energ a de $E$, lo que se asocia con $\Omega(E)$ estados.

Dado que la energ a total es $E_0$, el segundo sistema solo puede tener la energ a $E_0-E$ y un n mero de estados $\Omega(E_0-E)$ asociados.

Una vez que los ponemos en contacto, pueden intercambiar energ a hasta alcanzar alg n equilibrio. En este sentido, el valor de $E$ va a variar, y la probabilidad de encontrar los sistemas de modo que el primero tenga un valor de $E$ tambi n variar .

(ID 11541)

Comparando las curvas de n mero de estados

Si comparamos c mo var a el n mero de estados con la energ a $E$, notaremos que el comportamiento del sistema y del reservorio es inverso:

Esto ocurre porque al aumentar la energ a del sistema, la del reservorio disminuye, lo que a su vez reduce el n mero de estados a los que puede acceder.

(ID 11542)

Formaci n de un m ximo

Si multiplicamos el n mero de casos, obtenemos una funci n con un m ximo muy definido.

El sistema tendr una mayor probabilidad de encontrarse en la energ a en la que se encuentra el pico de la curva de probabilidad.

(ID 11543)

ID:(436, 0)