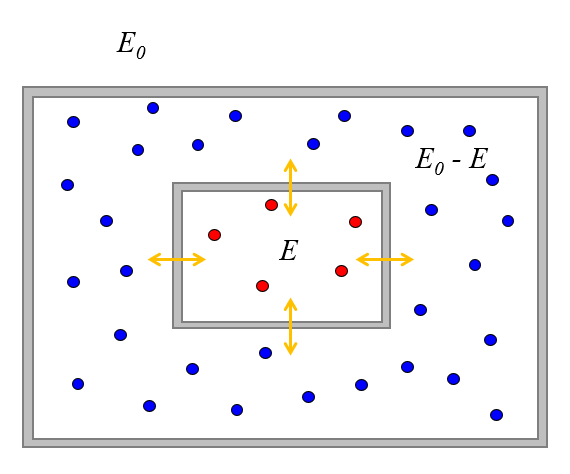
Podemos estudar o que acontece quando colocamos dois sistemas de part culas em contato, de modo que possam trocar energia, mas n o part culas.

Vamos tamb m supor que o sistema est isolado do ambiente, o que significa que possui uma energia total de $E_0$.

Suponhamos que inicialmente o primeiro sistema tenha uma energia de $E$, o que est associado a $\Omega(E)$ estados.

Uma vez que a energia total $E_0$, o segundo sistema s pode ter energia $E_0-E$ e um n mero de estados associados $\Omega(E_0-E)$.

Quando os colocamos em contato, eles podem trocar energia at atingir algum equil brio. Nesse sentido, o valor de $E$ vai variar, e a probabilidade de encontrar os sistemas de modo que o primeiro tenha um valor de $E$ tamb m vai variar.

(ID 11541)

Quando comparamos como o n mero de estados varia com a energia $E$, observamos que o comportamento do sistema e do reservat rio oposto:

Isso ocorre porque, medida que a energia aumenta, a energia do reservat rio diminui, o que por sua vez reduz o n mero de estados aos quais ele pode acessar.

(ID 11542)

Quando multiplicamos o n mero de casos, obtemos uma fun o com um pico muito pronunciado.

O sistema tem uma probabilidade maior de ser encontrado na energia onde ocorre o pico da curva de probabilidade.

(ID 11543)