Camino Libre

Storyboard

ID:(587, 0)

Partículas en un Volumen

Imagen

Conceptos

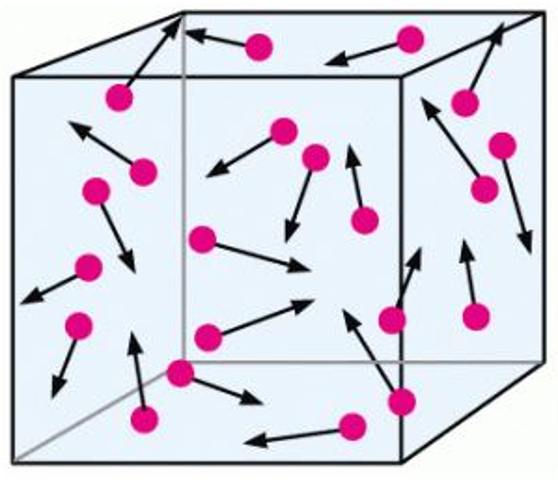
ID:(2051, 0)

Choque de partículas formando el camino libre

Imagen

Camino Libre

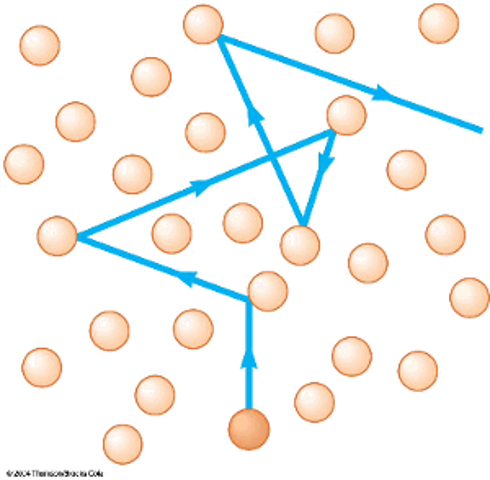
ID:(2052, 0)

Probabilidad de no Chocar

Ecuación

A medida que la partícula avanza con una velocidad v recorrerá en un tiempo dt la distancia dl. Si la probabilidad de choque por unidad de tiempo es \omega entonces la probabilidad de choque en el tiempo dt será \omega dt. Por ello la probabilidad de que no sufra choque en el tiempo dt es 1-\omega dt. Si P(t) es la probabilidad de que la partícula ha permanecido el tiempo t sin chocar entonces la probabilidad de que tras el tiempo t+dt no haya chocado es igual a\\n\\n

$P(t+dt)=(1-\omega dt)P(t)$

\\n\\nSi de desarrolla la probabilidad en dt se obtiene la ecuación diferencial para P(t):\\n\\n

$\displaystyle\frac{1}{P}\displaystyle\frac{dP}{dt}=-\omega$

Si se integra esta ecuación se obtiene con la probabilidad de que una partícula permanezca un tiempo t sin chocar contra:

ID:(4193, 0)

Probabilidad de chocar

Ecuación

Como la probabilidad de no chocar es con probabilidad de no chocar $-$, probabilidad de no chocar por unidad de tiempo $-$ y tiempo $s$

\\n\\nla probabilidad de chocar entre el tiempo t y t+dt es igual a\\n\\n

${\cal P}dt=P(t)-P(t+dt)=-\displaystyle\frac{dP}{dt}dt$

Con la probabilidad de no chocar antes indicada la probabilidad de chocar entre el tiempo t y t+dt es con probabilidad de no chocar $-$, probabilidad de no chocar por unidad de tiempo $-$ y tiempo $s$

ID:(4194, 0)

Tiempo medio entre choques

Ecuación

Con la probabilidad de chocar entre el tiempo t y t+dt se puede estimar el tiempo medio entre choque y choque con\\n\\n

$\tau=\displaystyle\int_0^{\infty}e^{-\omega t}\omega t dt$

lo que arroja con

ID:(4195, 0)

Cálculo del camino libre

Ecuación

Si la velocidad de la partícula es v y el tiempo medio entre choque y choque \tau entonces el camino libre sera con

ID:(4196, 0)

Angulo en que se desvía la partícula

Imagen

Sección eficaz total

ID:(2053, 0)

Sección eficaz total y tiempo entre colisiones

Ecuación

Si el tiempo medio entre dos colisiones es \tau y la velocidad relativa entre las partículas que colisionan \bar{V} el camino recorrido sera \\n\\n

$\bar{V}\tau$

\\n\\nComo la sección eficaz total \sigma_0 es equivalente a la sección que ofrece una partícula para ser impactada, el volumen\\n\\n

$\sigma_0\bar{V}\tau$

\\n\\nes tal que solo contendrá la partícula impactada. Por ello, si la concentración es c_N se debe dar que\\n\\n

$\sigma_0\bar{V}\tau c_N=1$

Con ello el tiempo medio entre dos choques consecutivos será con igual a

ID:(4197, 0)

Sección eficaz total y camino libre

Ecuación

Cuando las partículas se mueven la velocidad v pasa a ser la diferencia de la velocidad de ambas partículas\\n\\n

$\vec{V}=\vec{v}_2-\vec{v}_1$

\\n\\nSu valor medio sera por ello\\n\\n

$\bar{V}=\sqrt{v_1^2+v_2^2-2\vec{v}_1\cdot\vec{v}_2}$

\\n\\nComo no existe una dirección privilegiada se puede asumir que\\n\\n

$\vec{v}_1\cdot\vec{v}_2\sim 0$

\\n\\ny como\\n\\n

$v_1^2\sim v_2^2\sim v^2$

\\n\\ncon v la velocidad media de cada partícula, la velocidad relativa es\\n\\n

$\bar{V}=\sqrt{2}v$

Como el camino libre es con camino libre $m$, tiempo medio entre choques $s$ y velocidad media en una dirección $m/s$

y el tiempo entre choques con concentración $1/m^3$, sección eficaz total $m^2$, tiempo medio entre choques $s$ y velocidad relativa media $m/s$

se tiene que con el promedio de velocidad relativa con concentración $1/m^3$, sección eficaz total $m^2$, tiempo medio entre choques $s$ y velocidad relativa media $m/s$

ID:(4198, 0)