Processing math: 100%
Benützer: Keine Benutzer angemeldet.


Gaußsche Verteilung
Storyboard

In der Grenze ähnlicher Wahrscheinlichkeiten wird die Binomialverteilung in der kontinuierlichen Grenze zur Gaußschen Verteilung reduziert.

>Modell

ID:(1556, 0)


Distribución binomial
Gleichung

>Top, >Modell


Con la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}



con el número total de pasos es

N=n_1+n_2



y solo existe la probabilidad de ir a la derecha o a la izquierda, con se tiene para las probabilidades que

p+q=1



por lo que con se tiene la distribución binomial

W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }

ID:(8961, 0)


Ansatz für N!
Gleichung

>Top, >Modell


Mit der Stirling-Näherung

equation=8966

und die Änderung von Variablen

equation=8996

du verstehst das

equation

ID:(8998, 0)


Annäherung für n!
Gleichung

>Top, >Modell


Mit der Stirling-Näherung

equation=8966

und die Änderung von Variablen

equation=11431

du verstehst das

equation

ID:(9003, 0)


Annäherung für (N-n)!
Gleichung

>Top, >Modell


Mit der Stirling-Näherung

equation=8966

und die Änderung von Variablen

equation=8997

der Ausdruck ist

equation

ID:(8999, 0)


Factor N!/N!(N-n)! For N\gg 1, n\gg 1 and N>n
Gleichung

>Top, >Modell


Bei mittleren Wahrscheinlichkeiten p \sim q \sim 1/2 ) und großen Zahlen N kann dies angezeigt werden

N!\sim\sqrt{2\pi N}\left(\displaystyle\frac{N}{e}\right)^N



n!\sim\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^n



und

(N-n)!\sim\sqrt{2\pi(N-n)}\left(\displaystyle\frac{N-n}{e}\right)^{N-n}



bekommst

\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}

ID:(507, 0)


Grenze von großen Zahlen und mittleren Wahrscheinlichkeiten
Gleichung

>Top, >Modell


Der Ausdruck

W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }



wird reduziert um

\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}



zur Darstellung

W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}

ID:(506, 0)


Durchschnittliche Position
Gleichung

>Top, >Modell


Wenn insgesamt N Schritte mit einer Wahrscheinlichkeit p in der richtigen Richtung ausgeführt werden und diese eine Länge a haben, ist die erwartete Endposition

\mu=aNp

ID:(9008, 0)


Ändern Sie die Variablen durch Versatz von x=(n-Np)a
Gleichung

>Top, >Modell


Um die Gaußsche Verteilung zu erhalten, ist es notwendig, die Verteilung um ihre Abweichung von ihrer mittleren Position zu entwickeln, die durch gegeben sein kann

x=(n-Np)a

ID:(8973, 0)


Faktor n/N abhängig vom Weg x
Gleichung

>Top, >Modell


Wie der Weg ist

x=(n-Np)a



Faktor n/N kann geschrieben werden als

\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)

ID:(9004, 0)


Faktor N-n/N abhängig vom Weg x
Gleichung

>Top, >Modell


Wie der Weg ist

x=(n-Np)a



Faktor n/N kann geschrieben werden als

\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)

ID:(9005, 0)


Binomialverteilung als Funktion der Abweichung
Gleichung

>Top, >Modell


Wenn große Zahlen und Wahrscheinlichkeiten um 1/2 in die Binomialverteilung für den Fall eingegeben werden

W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}



die Ausdrücke

\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)



und

\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)




Man erhält eine Verteilung der Form

W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}p(1-p)}\left(1+\displaystyle\frac{x}{aNp}\right)^{-n-1/2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)^{-N+n-1/2}

ID:(8974, 0)


Variablenänderung u=x/aNp
Gleichung

>Top, >Modell


Um den Faktor 1+x/aNp zu entwickeln, können Sie mit der Variablenänderung arbeiten

u=\displaystyle\frac{x}{aNp}

ID:(9021, 0)


Faktor 1+x/aNp für N\gg 1 und p\sim 1/2
Gleichung

>Top, >Modell


Mit der Annäherung

1+u\sim e^{u-\frac{1}{2}u^2}



es muss

\left(1+\displaystyle\frac{x}{aNp}\right)\sim e^{x/aNp-x^2/2a^2N^2p^2}

ID:(9006, 0)


Variablenänderung u=x/aN(1-p)
Gleichung

>Top, >Modell


Um den Faktor 1+x/aN(1-p) zu entwickeln, können Sie mit der Variablenänderung arbeiten

u=\displaystyle\frac{x}{aN(1-p)}

ID:(9022, 0)


Faktor 1-x/aN(1-p) für N\gg 1 und p\sim 1/2
Gleichung

>Top, >Modell


Mit der Annäherung

1+u\sim e^{u-\frac{1}{2}u^2}



es muss

\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\sim e^{-x/aN(1-p)-x^2/2a^2N^2(1-p)^2}

ID:(9007, 0)


Wahrscheinlichkeit für große N und mittlere p
Gleichung

>Top, >Modell


Es kann gezeigt werden, dass für eine große Anzahl N und eine Wahrscheinlichkeit p, die weder zu klein noch zu nahe bei 1 liegt, die Binomialverteilung für die Position auf einen Gaußschen Wert reduziert wird x= na:

P(x)=\displaystyle\frac{1}{\sqrt{2\pi N^2p(1-p)}}e^{-(x-aNp)^2/2N^2p(1-p)}

In diesem Fall wurde die Wahrscheinlichkeit q durch 1-p ersetzt.

ID:(3367, 0)


Generalisierung der Grenzwerte für Big Numbers
Gleichung

>Top, >Modell


$\begin{matrix}

P(x) & = & \displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}\\

\sigma^2 & = & Np(1-p)\\

\end{matrix}

$

ID:(3368, 0)


Standardabweichung der Gaußschen Verteilung
Gleichung

>Top, >Modell


Die Standardabweichung der Binomialverteilung an der Grenze N groß und p mittel ist

\sigma^2 = N ^2 p (1- p )

ID:(8963, 0)


Beispielvergleich mit der Gaußschen Verteilung
Bild

>Top


Wenn wir die Binomialverteilung für große Zahlen N und Wahrscheinlichkeiten um 1/2 untersuchen

P(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}



welches unten dargestellt ist:

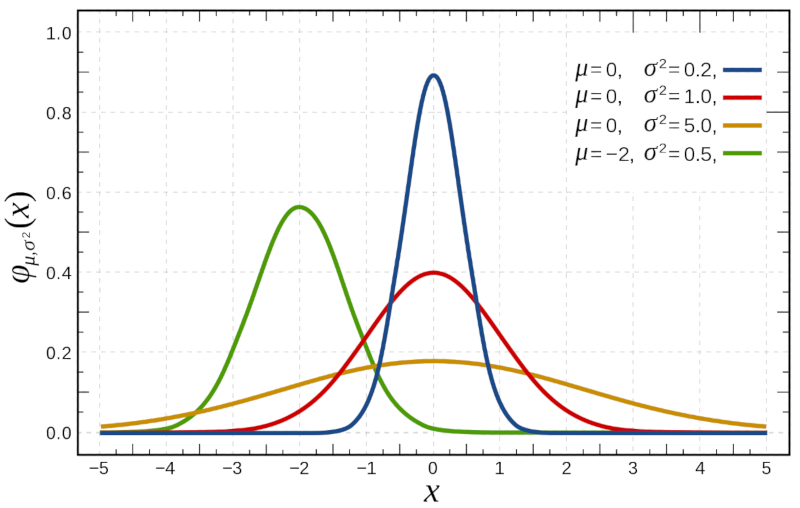
ID:(7793, 0)


0
Video

Video: Gaußsche Verteilung