Partikel in einer Box und Kugel
Storyboard 
Wenn wir ein Teilchen in einem Volumen, sei es eine Box oder eine Kugel, betrachten, können wir die Wahrscheinlichkeit abschätzen, das Teilchen in einem Bereich von Positionen zu finden.
ID:(433, 0)
Phasenraum eines Teilchens in einer Box 1D
Definition 
Stellen Sie sich eine Box mit der Länge
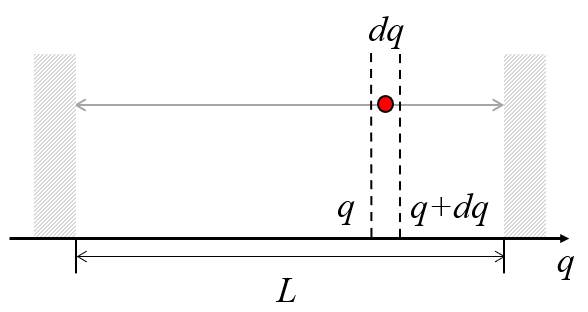
Die Frage ist, wie hoch die Wahrscheinlichkeit ist, sie in einem
ID:(11463, 0)
Phasenraum eines Teilchens in einer Box 2D
Bild 
Stellen Sie sich eine 2D-Box mit der Länge
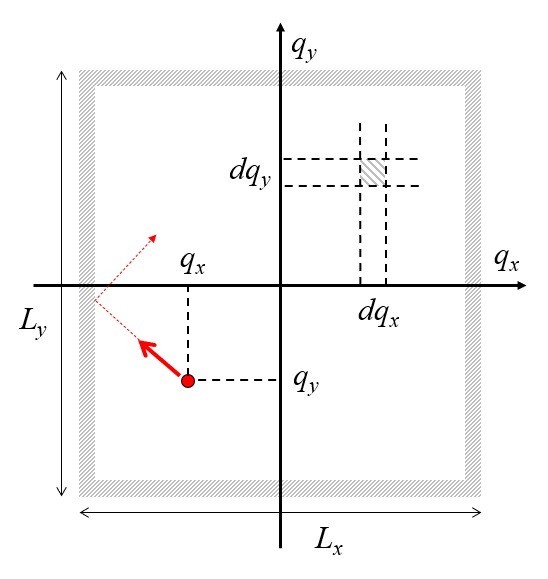
Die Frage ist, wie hoch die Wahrscheinlichkeit ist, sie in einem Viereck mit der Breite
ID:(11464, 0)
Phasenraum eines Teilchens in einer 3D-Kugel
Notiz 
Stellen Sie sich eine Kugel mit dem Radius
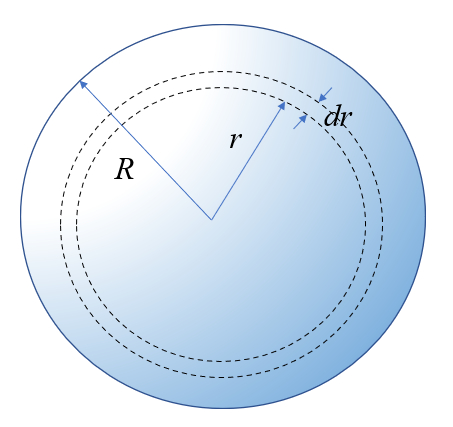
Die Frage ist, wie wahrscheinlich es ist, dass es in einer Schicht mit der Breite
ID:(11465, 0)
Wahrscheinlichkeit, das Teilchen in einem Radius $r$ zu finden
Zitat 
La probabilidad de encontrar la partícula en un radio entre
| $ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $ |
que se muestra en la siguiente gráfica:

ID:(11466, 0)
Partikel in einer Box und Kugel
Beschreibung 
Wenn wir ein Teilchen in einem Volumen, sei es eine Box oder eine Kugel, betrachten, können wir die Wahrscheinlichkeit abschätzen, das Teilchen in einem Bereich von Positionen zu finden.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Stellen Sie sich eine Box mit der L nge

Die Frage ist, wie hoch die Wahrscheinlichkeit ist, sie in einem
(ID 11463)
Si se asume que la part cula puede estar en cualquiera posici n en una dimensiones, las posiciones posibles son aquellas descritas por el largo
Las posiciones favorables de encontrar la part cula entre
| $ P(q) = \displaystyle\frac{1}{ L } dq $ |
Esto es solo valido si:
Toda posici n es igualmente probable.
lo que se puede generalizar en
Todo estado es igualmente probable.
Adicionalmente se debe notar que la probabilidad esta ntimamente ligada con el rango. Si el rango es nulo, tambi n lo es la probabilidad.
(ID 11476)
Stellen Sie sich eine 2D-Box mit der L nge

Die Frage ist, wie hoch die Wahrscheinlichkeit ist, sie in einem Viereck mit der Breite
(ID 11464)
Si se asume que la part cula puede estar en cualquiera posici n en dos dimensiones, las posiciones posibles son aquellas descritas por los largos de las aristas del rect ngulo.
Por ello la probabilidad de encontrar la part cula en el elemento rectangular son con igual a
| $ P(q_x,q_y) = \displaystyle\frac{1}{ L_x L_y } dq_x dq_y $ |
(ID 11475)
Stellen Sie sich eine Kugel mit dem Radius

Die Frage ist, wie wahrscheinlich es ist, dass es in einer Schicht mit der Breite
(ID 11465)
Si se asume que la part cula puede estar en cualquiera posici n tridimensional dentro de una esfera de radio
$4\pi r^2 dr$
\\n\\ndividido por el volumen de la esfera\\n\\n
$\displaystyle\frac{4\pi}{3} R^3$
por lo que con resulta la probabilidad igual a:
| $ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $ |
(ID 11474)
La probabilidad de encontrar la part cula en un radio entre
| $ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $ |
que se muestra en la siguiente gr fica:

(ID 11466)
ID:(433, 0)
