User:
Refraction when crossing a Flat Body
Storyboard 
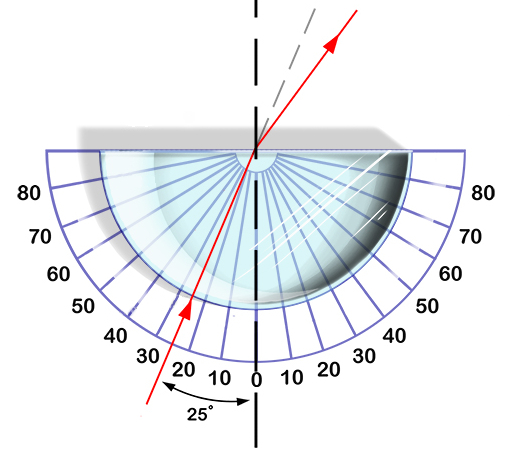
When the beam strikes a flat medium of defined interposed thickness, it penetrates with a different angle of refraction from the incident. This may be both greater and less than the angle of incidence depending on the respective refractive indices. Once the beam reaches the second edge of the medium, the process is reversed so that the beam returns to its original direction, only out of date.
ID:(1375, 0)
Snell's Law and Refraction Index
Equation
La ley de Snell para el paso de la luz de un medio de indice
 $ n_i \sin \theta_i = n_e \sin \theta_r $ |
Como la relación entre los ángulos de incidencia y refracción es
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
y el indice de refracción se define como
| $ n =\displaystyle\frac{ c }{ v }$ |
\\n\\nse tiene que con\\n\\n
$n_i=\displaystyle\frac{c}{c_i}$
y\\n\\n
$n_e=\displaystyle\frac{c}{c_e}$
\\n\\nque\\n\\n
$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$
por lo que resulta
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
ID:(3343, 0)
Displacement
Equation
Para calcular la distancia
Para obtener
y se puede obtener
Con ello se obtiene
| $ d = h \displaystyle\frac{\sin( \theta_1 - \theta_2 )}{\cos \theta_1 }$ |
ID:(3345, 0)