Usuario:
Refracción al atravesar un Cuerpo Plano
Storyboard 
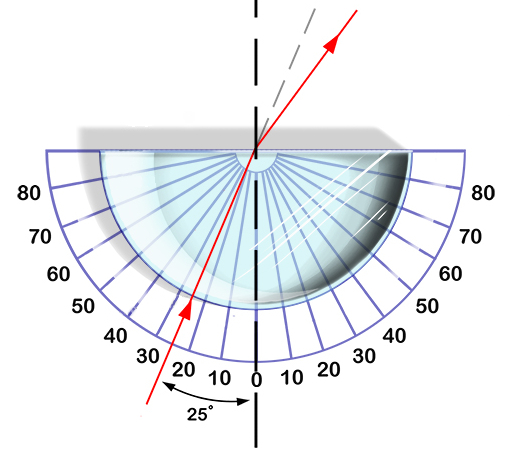
Cuando el haz incide sobre un medio plano de grosor definido interpuesto penetra con un angulo de refracción distinto al incidente. Este puede ser tanto mayor como menor al anglo de incidencia dependiendo de los respectivos indices de refracción. Una vez el haz alcanza el segundo borde del medio el proceso se invierte con lo que el haz vuelve a su dirección original solo que desfasado.
ID:(1375, 0)
Ley de Snell en función del índice de refracción
Ecuación
La ley de Snell para el paso de la luz de un medio de indice
 $ n_i \sin \theta_i = n_e \sin \theta_r $ |
Como la relación entre los ángulos de incidencia y refracción es
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
y el indice de refracción se define como
| $ n =\displaystyle\frac{ c }{ v }$ |
\\n\\nse tiene que con\\n\\n
$n_i=\displaystyle\frac{c}{c_i}$
y\\n\\n
$n_e=\displaystyle\frac{c}{c_e}$
\\n\\nque\\n\\n
$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$
por lo que resulta
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
ID:(3343, 0)
Desplazamiento
Ecuación
Para calcular la distancia
Para obtener
y se puede obtener
Con ello se obtiene
| $ d = h \displaystyle\frac{\sin( \theta_1 - \theta_2 )}{\cos \theta_1 }$ |
ID:(3345, 0)