Storyboard

When the light passes from a medium with a high index of refraction (low speed) to one with a lower index of refraction (higher speed) the beam is refracted at a greater angle than the normal interface. This leads to the fact that for a certain angle of finite incidence the angle of refraction reaches 90 degrees making it impossible for the beam to pass to the second medium. That leads to the beam experiencing a total internal refraction.

>Model

ID:(1262, 0)

Description

>Top

Cuando la luz en un medio con velocidad de la luz c_i alcanza una medio con una velocidad de la luz c_e el haz en en parte reflejado y en parte transmitido.

La transmisión sin embargo no solo puede perder intensidad, por la fracción reflejada, también puede ser desviada. Este desvío se denomina refracción.

ID:(429, 0)

Image

>Top

Paso de medio con mayor a menor velocidad

ID:(1849, 0)

Image

>Top

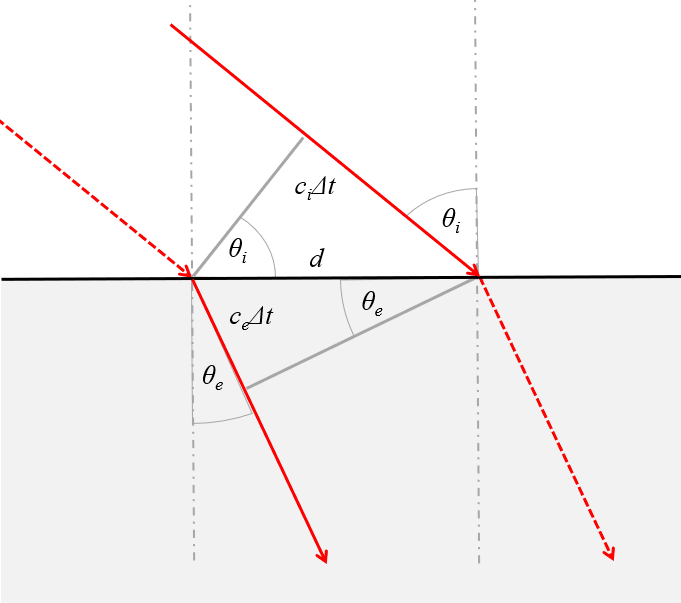
Cuando un haz pasa de un medio de menor velocidad v_i a uno con mayor v_e su dirección se altera de modo que el angulo de incidencia \theta_i se agranda:

ID:(1850, 0)

Image

>Top

Cuando se pasa de un medio en que la velocidad de la luz es menor a uno que es mayor existe la situación de que a un ángulo de incidencia muy grande no existe un correspondiente angulo de refracción. En estos casos la luz solo se refleja y hablamos de reflexión total.

En la siguiente imagen se ven distintos haces que al llegar a ser muy grande el angulo comienzan a sufrir reflexión total:

ID:(1851, 0)

Equation

>Top, >Model

La ley de Snell para el paso de la luz de un medio de indice n_i bajo un ángulo \theta_i a un medio de indice n_e en que se refracta bajo un angulo \theta_e se escribe como:

$ n_i \sin \theta_i = n_e \sin \theta_r $

Conditions

Variables

$\theta_i$

Angulo de incidente

$rad$

5147

$\theta_r$

Angulo de refracción

$rad$

5148

$n_i$

Indice de refracción en el medio incidente

$-$

5145

$n_e$

Refractive Index over the Medium 1 to Medium 2

$-$

5146

Relation

Development

Como la relación entre los ángulos de incidencia y refracción es

$\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$

y el indice de refracción se define como

$ n =\displaystyle\frac{ c }{ v }$

\\n\\nse tiene que con\\n\\n

$n_i=\displaystyle\frac{c}{c_i}$

y\\n\\n

$n_e=\displaystyle\frac{c}{c_e}$

\\n\\nque\\n\\n

$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$

por lo que resulta

$ n_i \sin \theta_i = n_e \sin \theta_r $

ID:(3343, 0)

Equation

>Top, >Model

Cuando la luz pasa de un medio de menor a mayor velocidad se puede dar la situación de que el angulo de incidencia es tan grande que no existe un angulo de refracción ya que este tiene que ser mayor que el incidente y no puede ser mayor que 90 grados (\pi/2). En ese limite, en que \theta_r=\pi/2 el angulo incidente es igual a

$\sin \theta_c =\displaystyle\frac{ n_e }{ n_i }$

Conditions

Variables

$\theta_c$

Angulo de reflexión total

$rad$

5149

$n_i$

Indice de refracción en el medio incidente

$-$

5145

$n_e$

Refractive Index over the Medium 1 to Medium 2

$-$

5146

Relation

Development

En el caso de reflexión total el ángulo de refracción es \theta_e=\pi/2 y con ello el seno igual a uno. Empleando la ley de Snell

$ n_i \sin \theta_i = n_e \sin \theta_r $

\\n\\npodemos calcular el ángulo de incidencia \theta_i, que definimos como ángulo crítico \theta_c, con:\\n\\n

$n_i\sin\theta_c=n_e$

por lo que se puede escribir

$\sin \theta_c =\displaystyle\frac{ n_e }{ n_i }$

ID:(3344, 0)

Equation

>Top, >Model

Como la reflexión total esta dada por

se puede expresar esta relación mediante los indices de refracción como

$ sin \theta_c =\displaystyle\frac{ c_i }{ c_e }$

Conditions

Variables

$\theta_c$

Angulo de reflexión total

$rad$

5149

$c_i$

Velocidad de la luz en el medio incidente

$m/s$

9822

$c_e$

Velocidad de la luz en el medio refractado

$m/s$

9823

Relation

Development

En el caso de reflexión total

$\sin \theta_c =\displaystyle\frac{ n_e }{ n_i }$

se puede reescribir en función de la velocidad de la luz en el medio c_i y c_e si se recuerda que el indice de refracción es

$ n =\displaystyle\frac{ c }{ v }$

\\n\\nse tiene que\\n\\n

$\sin\theta_c=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{c}{c_e}=\displaystyle\frac{c_i}{c}=\displaystyle\frac{c_i}{c_e}$

a la relación

$ sin \theta_c =\displaystyle\frac{ c_i }{ c_e }$

ID:(9782, 0)

Image

>Top

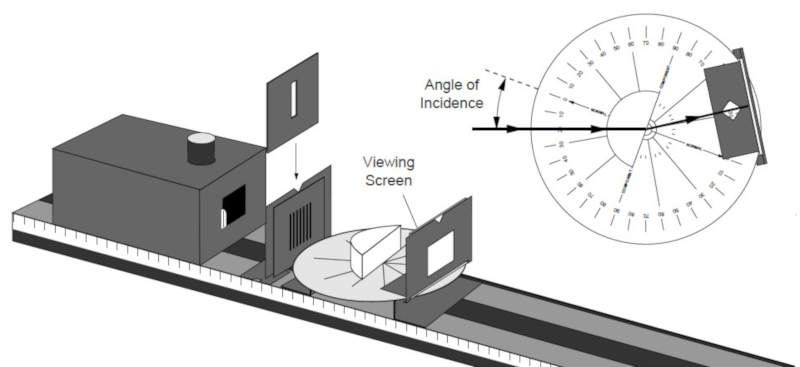
If the beam in a medium of less speed tries to move to a medium of greater speed in an angle such that there is no refractive angle this is fully reflected in the interface between both means.

ID:(1852, 0)

Image

>Top

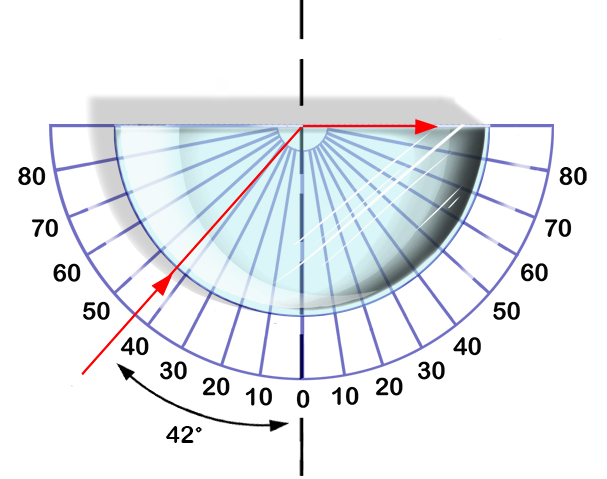
En el caso de que se pase de un sistema de menor a mayor velocidad existe la situación en que el haz transmitido, que tiene que ser siempre mayor al incidente, llegue a ser 90 grados. Si en esa situación se continua aumentando el angulo de incidencia se observara que el haz comienza a reflejarse bajo el mismo angulo que incidió:

Este fenómeno se denomina refracción total.

ID:(12675, 0)

Image

>Top

Si consideramos lo que vera un buso debajo del agua veremos que ...

• Existe un cono en que no existe refracción total que esta sobre el. Esto porque al mirar hacia arriba la luz que viene dentro del agua logra 'escapar' porque su angulo respecto de la normal es menor que el angulo critico. Por esta razón en esta dirección vemos lo que esta fuera del agua.
• Fuera del cono todo lo que esta dentro del agua se refleja en la superficie. Esta opera como un espejo mostrando todo en forma invertida y se superpone con lo que se ve dentro del agua (como por ejemplo la ola en la superficie).
&bull: Adicional a lo que se ve reflejado en la superficie el buzo ve lo que esta dentro del agua.

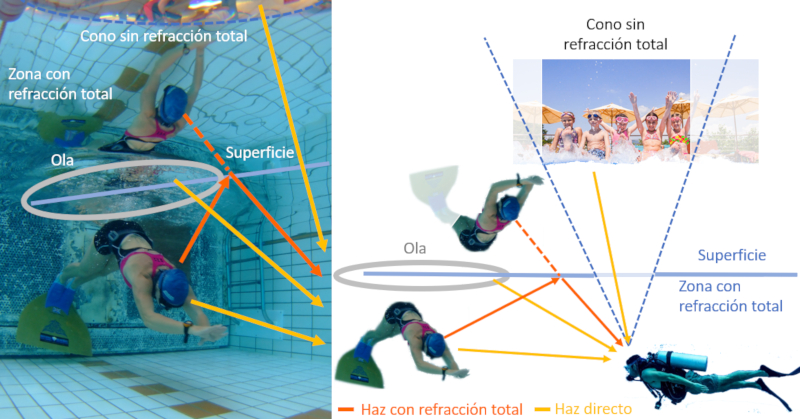
Como la velocidad de la luz en el agua es 2.2541e+8 m/s y en el aire 2.9979e+8 m/s es se puede calcular el angulo de refracción total. Este resulta con un valor de 48.5 lo que muestra que el cono es una sección no menor de la superficie.

ID:(12680, 0)

0

Video

Video: Reflexión Total