Benützer:
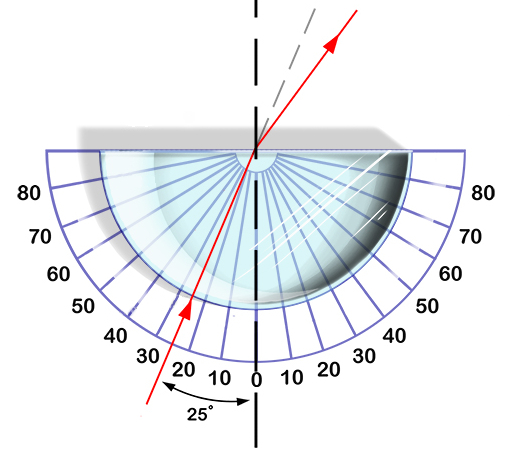
Brechung beim Überqueren eines flachen Körpers
Storyboard 
Wenn der Strahl auf ein flaches Medium mit definierter dazwischenliegender Dicke trifft, dringt er mit einem anderen Brechungswinkel als der einfallende ein. Dies kann in Abhängigkeit von den jeweiligen Brechungsindizes sowohl größer als auch kleiner als der Einfallswinkel sein. Sobald der Strahl die zweite Kante des Mediums erreicht, wird der Vorgang umgekehrt, sodass der Strahl nur veraltet in seine ursprüngliche Richtung zurückkehrt.
ID:(1375, 0)
Snells Gesetz und Brechungsindex
Gleichung
La ley de Snell para el paso de la luz de un medio de indice
 $ n_i \sin \theta_i = n_e \sin \theta_r $ |
Como la relación entre los ángulos de incidencia y refracción es
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
y el indice de refracción se define como
| $ n =\displaystyle\frac{ c }{ v }$ |
\\n\\nse tiene que con\\n\\n
$n_i=\displaystyle\frac{c}{c_i}$
y\\n\\n
$n_e=\displaystyle\frac{c}{c_e}$
\\n\\nque\\n\\n
$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$
por lo que resulta
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
ID:(3343, 0)
Verschiebung
Gleichung
Para calcular la distancia
Para obtener
y se puede obtener
Con ello se obtiene
| $ d = h \displaystyle\frac{\sin( \theta_1 - \theta_2 )}{\cos \theta_1 }$ |
ID:(3345, 0)