Usuario:
Emisión de una fuente puntual
Storyboard 
Emisión de una fuente puntual
En el caso de la emisión desde una fuente puntual no existe una direccón priveligiada por lo que la emisión es isotropica o sea igual en todas las diección.
Si se piensa la luz como particulas se vera que su numero, y por ello su intensidad se reducira con el inverso del radio al cuadrado por efecto que los fotones se reparten en una superficie cada vez mas grande.
ID:(300, 0)
Luz
Imagen
La luz es una onda electromagnética con una longitud de onda $\lambda$ que se encuentra en un rango entre 380 nm y 750 nm, dentro del espectro visible que nuestro ojo es capaz de percibir.
La luz se propaga en línea recta y puede sufrir refracción, es decir, desviarse, si la velocidad de la luz cambia debido al medio que atraviesa.
ID:(408, 0)
Propagación de la luz en linea recta y en forma esférica
Imagen
La luz se propaga en línea recta y se distribuye en forma esférica alrededor de su fuente.
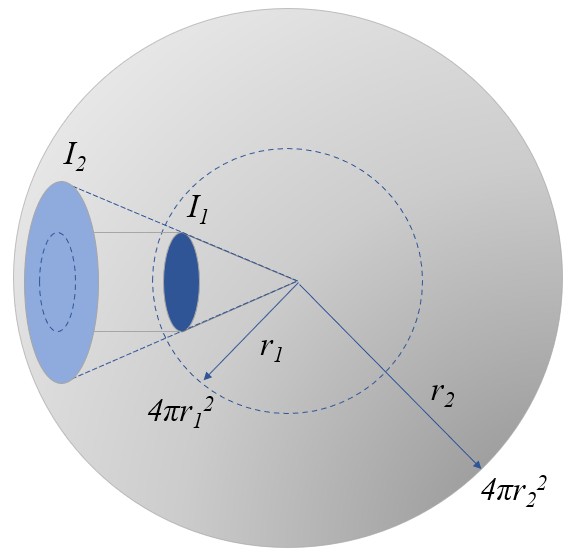
Debido a esta distribución esférica, su intensidad disminuye a medida que la luz se aleja de la fuente.
ID:(12677, 0)
Emisión no uniforme: orificio
Imagen
Cuando la luz atraviesa un orificio, no se propaga de manera uniforme, sino que presenta una distribución que da lugar a lo que se conoce como penumbra.
ID:(12679, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \Delta\Phi = I \Delta\Omega $
DPhi = I * Domega
$ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $
I_2 = r_2 ^2 * I_1 / r_1 ^2
$ \Phi =\displaystyle\int I d \Omega $
Phi =@INT( I , Omega )
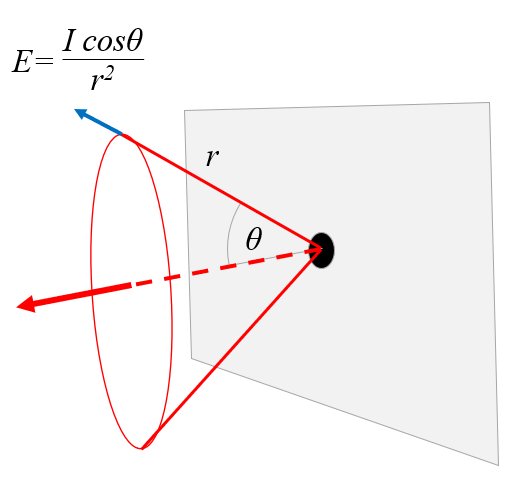
$E=\displaystyle\frac{I\cos\theta}{r^2}$
E=I*cos(theta)/r^2
ID:(16081, 0)
Reducción de la intensidad con la distancia
Ecuación
Si la luz emite en todas las direcciones de manera uniforme, se distribuirá de manera homogénea sobre la superficie de una esfera imaginaria con un área de
$4\pi r^2$
Por lo tanto, si conocemos su intensidad a una distancia $r_1$, podemos predecir su intensidad a una distancia $r_2$ utilizando
| $ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $ |
Dado que la cantidad de luz se conserva, la intensidad (energía por área) multiplicada por el área debe ser una constante, lo que nos lleva a la siguiente relación:
$4\pi r_1^2I_1=4\pi r_2^2I_2$
Por lo tanto, podemos expresar la relación entre las intensidades a diferentes distancias como:
| $ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $ |
ID:(12678, 0)
Flujo
Ecuación
El flujo radiativo ($\Phi$) se calcula a partir de la intensidad (
| $ \Delta\Phi = I \Delta\Omega $ |
y se expresa en vatios (W).
En el contexto en el que se evalúa el flujo teniendo en cuenta la capacidad del ojo humano para percibir la potencia luminosa, se utiliza la unidad de lumen (lm).
ID:(464, 0)
Flujo total
Ecuación
Dado que el flujo a través de un elemento de ángulo $d\Omega$ está definido como
| $ \Delta\Phi = I \Delta\Omega $ |
el flujo total se obtiene integrando la intensidad sobre toda la superficie, como se muestra en la siguiente expresión:
| $ \Phi =\displaystyle\int I d \Omega $ |
Si se quiere conocer el flujo total se debe sumar sobre toda la superficie. Esto es se debe integrar (=sumar) sobre toda la superficie de modo de
| $ \Delta\Phi = I \Delta\Omega $ |
lo que arroja
| $ \Phi =\displaystyle\int I d \Omega $ |
Algunos ejemplos de flujos totales incluyen:
Fuente | Flujo
Lámpara de alta presión de Xe | 3.0E+6 lm
Lámpara de arco | 1.0E+4 lm
Lámpara fluorescente de 65 W | 3.3E+3 lm
Bombilla de 60 W | 6.2E+2 lm
ID:(138, 0)
Irradiancia
Ecuación
Cuando una radiación de intensidad
| $E=\displaystyle\frac{I\cos\theta}{r^2}$ |
se mide en Lux (lx), lo que equivale a un lumen por metro cuadrado.
Para proporcionar una referencia de los valores de irradiancia en condiciones de luz natural, podemos considerar los siguientes valores:
Situación Irradiancia
Medio día, verano, soleado 1.0E+5 lx
Medio día, verano, nublado 2.0E+4 lx
Medio día, invierno, soleado 1.0E+4 lx
Medio día, invierno, nublado 2.0E+3 lx
ID:(8601, 0)