User:
Emisión de una fuente puntual
Storyboard 
The propagation of light in a homogeneous medium occurs rectilinearly at a characteristic speed that depends on both the medium and the frequency (color) of the light.
Propagation can be described both as a corpuscular model, in which the particles are called photons, as a wave model.
ID:(300, 0)
Light
Image
Light is an electromagnetic wave with a wavelength $\lambda$ that falls within the range of 380 nm to 750 nm, encompassing the visible spectrum that our eyes can perceive.
Light propagates in a straight line and can undergo refraction, meaning it can be deviated, if the speed of light changes due to the medium it passes through.
ID:(408, 0)
Propagation of light in a straight line and in a spherical shape
Image
Light travels in a straight line and radiates spherically around its source.
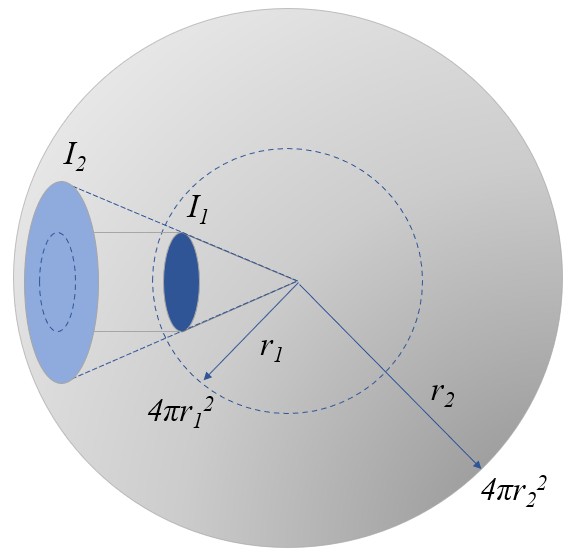
Because of this spherical distribution, its intensity decreases with distance from the source.
ID:(12677, 0)
Non-uniform emission: orifice
Image
When light passes through an aperture, it does not propagate uniformly but instead exhibits a distribution, creating what is known as a penumbra.
ID:(12679, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta\Phi = I \Delta\Omega $
DPhi = I * Domega
$ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $
I_2 = r_2 ^2 * I_1 / r_1 ^2
$ \Phi =\displaystyle\int I d \Omega $
Phi =@INT( I , Omega )
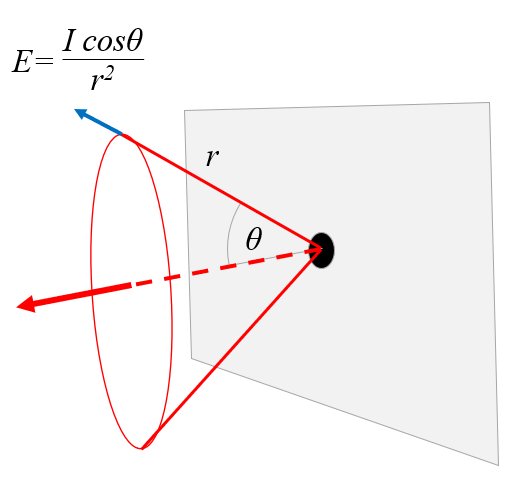
$E=\displaystyle\frac{I\cos\theta}{r^2}$
E=I*cos(theta)/r^2
ID:(16081, 0)
Reduction in intensity with distance
Equation
If light emits in all directions uniformly, it will distribute itself evenly over the surface of an imaginary sphere with an area of
$4\pi r^2$
Hence, if we know its intensity at a distance $r_1$, we can predict its intensity at a distance $r_2$ using
| $ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $ |
Since the amount of light is conserved, the intensity (energy per area) multiplied by the area must be a constant, which leads us to the following relationship:
$4\pi r_1^2I_1=4\pi r_2^2I_2$
Therefore, we can express the relationship between intensities at different distances as:
| $ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $ |
ID:(12678, 0)
Flow
Equation
Radiative flux ($\Phi$) is calculated from the intensity (
| $ \Delta\Phi = I \Delta\Omega $ |
and it is measured in watts (W).
In the context where flux is evaluated with respect to the human eye's ability to perceive luminous power, it is expressed in the unit of lumens (lm).
ID:(464, 0)
Total flow
Equation
Since the flux through an element of angle $d\Omega$ is defined as
| $ \Delta\Phi = I \Delta\Omega $ |
the total flux is obtained by integrating the intensity over the entire surface, as shown in the following expression:
| $ \Phi =\displaystyle\int I d \Omega $ |
Si se quiere conocer el flujo total se debe sumar sobre toda la superficie. Esto es se debe integrar (=sumar) sobre toda la superficie de modo de
| $ \Delta\Phi = I \Delta\Omega $ |
lo que arroja
| $ \Phi =\displaystyle\int I d \Omega $ |
Some examples of total flux include:
Source | Flux
High-Pressure Xenon Lamp | 3.0E+6 lm
Arc Lamp | 1.0E+4 lm
65W Fluorescent Lamp | 3.3E+3 lm
60W Bulb | 6.2E+2 lm
ID:(138, 0)
Irradiance
Equation
When radiation with intensity
| $E=\displaystyle\frac{I\cos\theta}{r^2}$ |
is measured in Lux (lx), which corresponds to one lumen per square meter.
For natural light, the following values can be used as reference:
Scenario Irradiance
Noon, summer, sunny 1.0E+5 lx
Noon, summer, cloudy 2.0E+4 lx
Noon, winter, sunny 1.0E+4 lx
Noon, winter, cloudy 2.0E+3 lx
ID:(8601, 0)