Benützer:
Emisión de una fuente puntual
Storyboard 
Die Ausbreitung von Licht in einem homogenen Medium erfolgt geradlinig mit einer charakteristischen Geschwindigkeit, die sowohl vom Medium als auch von der Frequenz (Farbe) des Lichts abhängt.
Die Ausbreitung kann sowohl als Korpuskularmodell, in dem die Teilchen Photonen genannt werden, als Wellenmodell beschrieben werden.
ID:(300, 0)
Licht
Bild
Licht ist eine elektromagnetische Welle mit einer Wellenlänge $\lambda$, die sich im Bereich von 380 nm bis 750 nm befindet und damit im sichtbaren Spektrum liegt, das unser Auge wahrnehmen kann.
Licht breitet sich geradlinig aus und kann brechend, also abgelenkt, werden, wenn sich die Geschwindigkeit des Lichts aufgrund des durchquerten Mediums ändert.
ID:(408, 0)
Lichtausbreitung geradlinig und kugelförmig
Bild
Licht breitet sich geradlinig aus und strahlt kugelförmig um seine Quelle herum.
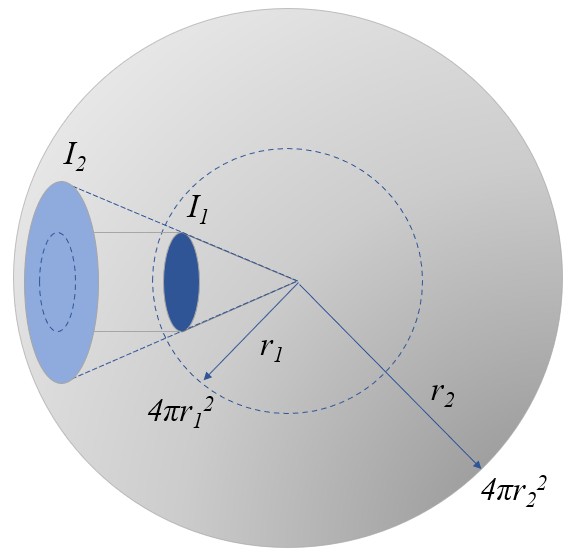
Aufgrund dieser kugelförmigen Verteilung nimmt seine Intensität mit der Entfernung von der Quelle ab.
ID:(12677, 0)
Ungleichmäßige Emission: Öffnung
Bild
Wenn Licht durch eine Öffnung dringt, breitet es sich nicht gleichmäßig aus, sondern zeigt eine Verteilung, die das erzeugt, was als Halbschatten bekannt ist.
ID:(12679, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta\Phi = I \Delta\Omega $
DPhi = I * Domega
$ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $
I_2 = r_2 ^2 * I_1 / r_1 ^2
$ \Phi =\displaystyle\int I d \Omega $
Phi =@INT( I , Omega )
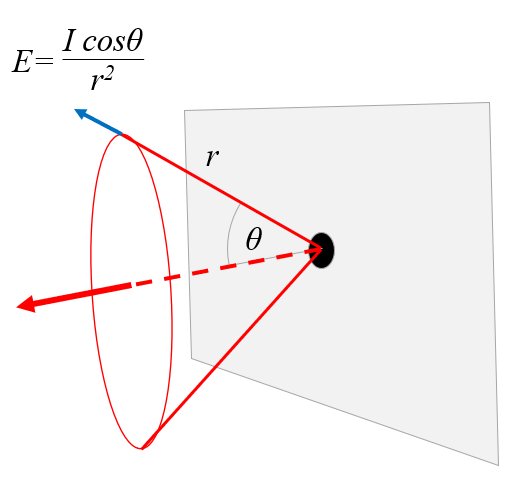
$E=\displaystyle\frac{I\cos\theta}{r^2}$
E=I*cos(theta)/r^2
ID:(16081, 0)
Verringerung der Intensität mit zunehmender Entfernung
Gleichung
Wenn das Licht gleichmäßig in alle Richtungen ausstrahlt, verteilt es sich gleichmäßig über die Oberfläche einer imaginären Kugel mit einer Fläche von
$4\pi r^2$
Daher können wir, wenn wir die Intensität in einem Abstand von $r_1$ kennen, die Intensität in einem Abstand von $r_2$ mit Hilfe von
| $ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $ |
Da die Menge an Licht erhalten bleibt, muss die Intensität (Energie pro Fläche) multipliziert mit der Fläche eine Konstante sein, was uns zu folgender Beziehung führt:
$4\pi r_1^2I_1=4\pi r_2^2I_2$
Daher können wir die Beziehung zwischen Intensitäten in verschiedenen Entfernungen wie folgt ausdrücken:
| $ I_2 =\displaystyle\frac{ r_1 ^2}{ r_2 ^2} I_1 $ |
ID:(12678, 0)
Fluss
Gleichung
Der Strahlungsfluss ($\Phi$) wird aus der Intensität (
| $ \Delta\Phi = I \Delta\Omega $ |
und wird in Watt (W) gemessen.
In dem Zusammenhang, in dem der Fluss unter Berücksichtigung der Fähigkeit des menschlichen Auges, die Lichtleistung wahrzunehmen, bewertet wird, wird er in der Einheit Lumen (lm) angegeben.
ID:(464, 0)
Gesamtdurchfluss
Gleichung
Da der Fluss durch ein Element des Winkels $d\Omega$ definiert ist als
| $ \Delta\Phi = I \Delta\Omega $ |
wird der Gesamtfluss durch Integration der Intensität über die gesamte Oberfläche erhalten, wie in folgendem Ausdruck dargestellt:
| $ \Phi =\displaystyle\int I d \Omega $ |
Si se quiere conocer el flujo total se debe sumar sobre toda la superficie. Esto es se debe integrar (=sumar) sobre toda la superficie de modo de
| $ \Delta\Phi = I \Delta\Omega $ |
lo que arroja
| $ \Phi =\displaystyle\int I d \Omega $ |
Einige Beispiele für den Gesamtfluss sind:
Quelle | Fluss
Hochdruck-Xenonlampe | 3.0E+6 lm
Bogenlampe | 1.0E+4 lm
65W Leuchtstofflampe | 3.3E+3 lm
60W Glühlampe | 6.2E+2 lm
ID:(138, 0)
Bestrahlung
Gleichung
Wenn Strahlung mit Intensität
| $E=\displaystyle\frac{I\cos\theta}{r^2}$ |
in Lux (lx) gemessen, was einem Lumen pro Quadratmeter entspricht.
Für natürliches Licht können die folgenden Werte als Referenz verwendet werden:
Szenario Bestrahlungsstärke
Mittags, Sommer, sonnig 1.0E+5 lx
Mittags, Sommer, bewölkt 2.0E+4 lx
Mittags, Winter, sonnig 1.0E+4 lx
Mittags, Winter, bewölkt 2.0E+3 lx
ID:(8601, 0)