Variación de calor especifico con la temperatura
Definición 
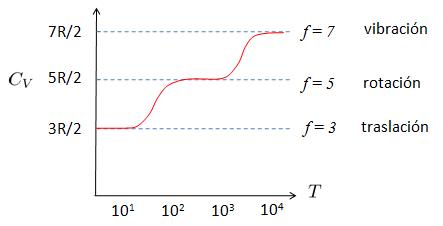
Variación de la capacidad calórica
ID:(1961, 0)
Capacidad calorífica
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
La capacidad cal rica es el calor o energ a
$\delta Q = C_V dT$
\\n\\nSi la energ a de
$U=\displaystyle\frac{f}{2}nN_Ak_BT$
\\n\\npor lo que, si el volumen se mantiene constante\\n\\n
$dU=\delta Q=\displaystyle\frac{f}{2}nN_Ak_BdT$
\\n\\npor lo que con\\n\\n
$R=k_BN_A$
se tiene
El calor especifico corresponde a la capacidad cal rica por masa
$c_V=\displaystyle\frac{C_V}{M}$
Si
$M=nN_Am$
con
$C_V=\displaystyle\frac{f}{2}nkN_A$
por lo que el calor especifico es
Variaci n de la capacidad cal rica
ID:(1618, 0)
