Usuario:
Camino libre en un gas
Concepto 
Cuando una partícula de un gas se desplaza, interactúa con las demás partículas en su entorno. La forma más simple de esta interacción es a través de choques elásticos, lo que significa que la partícula choca sin perder energía, cambiando su dirección para luego impactar con otra partícula.
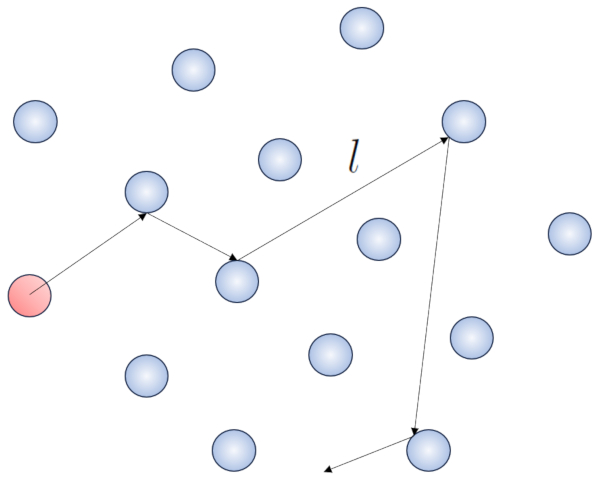
Dentro de este proceso, tiene sentido definir el camino libre ($\bar{l}$), cuyo valor dependerá de una concentración de particulas ($c_n$).
ID:(1708, 0)
Camino libre con movimiento de vecinos
Concepto
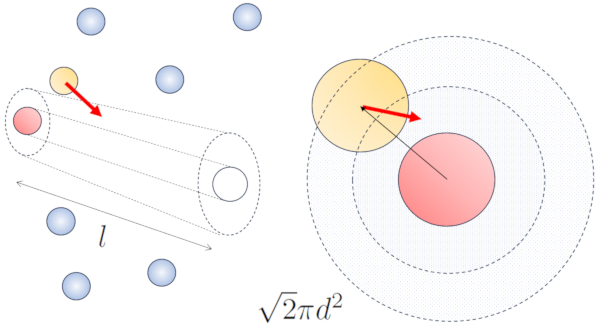
Cuando las partículas vecinas están en movimiento, existe una mayor probabilidad de colisión debido a que durante el mismo intervalo de tiempo, recorren una mayor distancia. Las componentes de velocidad, $v_x$, $v_y$, y $v_z$, fluctúan alrededor de valores medios $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ y $\sqrt{\langle v_z^2\rangle}$. Si asumimos que el sistema es isotrópico, el promedio de cada componente será igual a $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Por lo tanto, en el eje a lo largo del cual se desplaza la partícula, recorrerá una distancia
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
Al mismo tiempo, las partículas que se desplazan perpendicularmente habrán recorrido una distancia:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Por lo tanto, la probabilidad de colisión aumentará en un factor de $\sqrt{2}$ en comparación con el caso en el que las partículas no se desplazan:
ID:(1963, 0)
Camino libre medio para vecinos en reposo
Ecuación
Si
$l\pi d^2c_n=1$
o
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
ID:(3942, 0)
Camino libre sin movimiento de vecinos
Concepto
Cuando una partícula de un radio dado se desplaza en el espacio, efectivamente ocupa el espacio de un cilindro con el mismo radio. Para que esta partícula colisione con otra, esta segunda debe tener parte de su volumen dentro de dicho cilindro. En el caso más extremo, la segunda partícula se encuentra a una distancia de dos radios del primero, de manera que el borde del cilindro está en contacto con un punto de la esfera más cercano al eje del cilindro. El centro de esta esfera se encuentra a una distancia igual a un radio desde la superficie del cilindro:
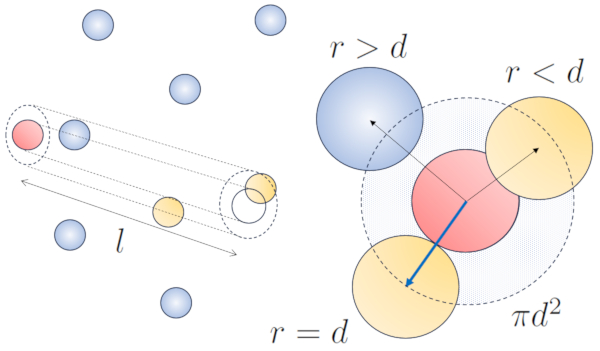
Por lo tanto, la distancia entre el eje del cilindro y el centro de cualquier partícula es de dos radios, es decir, un diámetro. En otras palabras, se puede concebir que el volumen ocupado de manera literal por la partícula que se desplaza en el espacio es un cilindro con una longitud igual al camino libre y un radio igual al diámetro de la propia partícula.
ID:(1962, 0)
Camino libre medio para vecinos en movimiento
Ecuación
Para el caso sin movimiento, la probabilidad es de el camino libre ($\bar{l}$), mientras que con movimiento, las probabilidades son de el diámetro de la partícula ($d$) y la concentración de particulas ($c_n$), respectivamente.
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
En el caso del movimiento, la probabilidad se incrementa en un factor de $\sqrt{2}$, lo que significa que el camino libre es
 $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)