User:
Free path in a gas
Concept 
When a particle of a gas moves, it interacts with other particles. The simplest form of this interaction is through elastic collisions, meaning that the particle collides without losing energy, changing its direction to impact another particle.
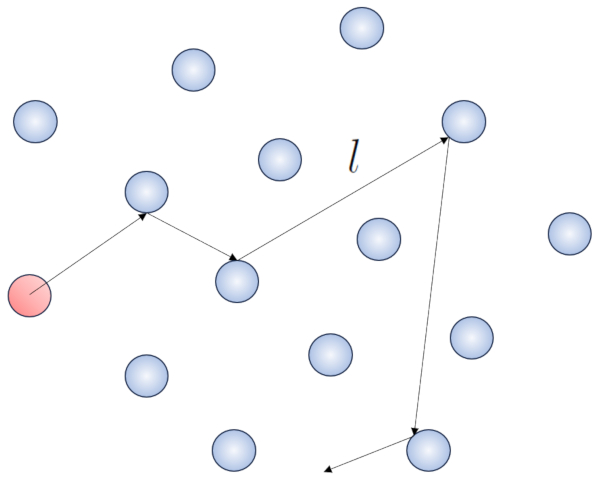
None
Within this process, it makes sense to define the free path ($\bar{l}$), whose value will depend on ($$).
ID:(1708, 0)
Free path with neighbors with movement
Concept
When neighboring particles are in motion, there is a higher probability of collision due to the fact that they cover a greater distance in the same amount of time. The velocity components, $v_x$, $v_y$, and $v_z$, fluctuate around mean values $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$, and $\sqrt{\langle v_z^2\rangle}$. Assuming the system is isotropic, the average of each component will be equal to $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Therefore, along the axis along which the particle is moving, it will travel a distance
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
At the same time, particles moving perpendicular will have covered a distance:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Hence, the collision probability increases by a factor of $\sqrt{2}$ compared to the case where the particles are not in motion:
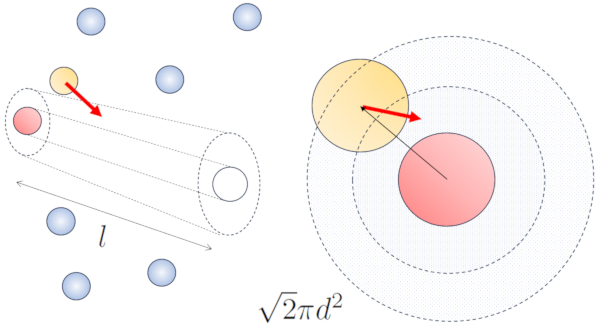
None
ID:(1963, 0)
Mean free path for resting neighbors
Equation
If
$l\pi d^2c_n=1$
or
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
ID:(3942, 0)
Free path with neighbors without movement
Concept
When a particle with a given radius moves through space, it effectively occupies the space of a cylinder with the same radius. For one particle to collide with another, the second particle must have some of its volume within this cylinder. In the most extreme case, the second particle is located at a distance of two radii from the first one, so that the edge of the cylinder touches a point on the sphere closest to the cylinder's axis. The center of this sphere is at a distance equal to one radius from the surface of the cylinder:
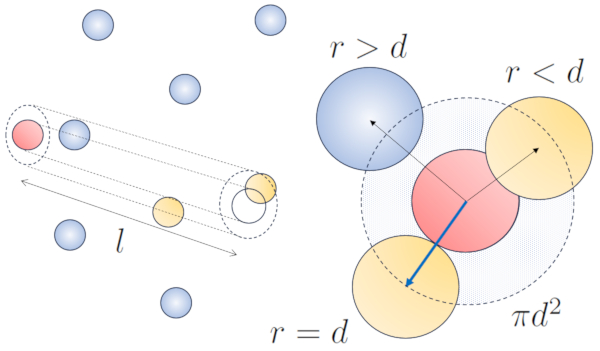
None
Therefore, the distance between the cylinder's axis and the center of any particle is two radii, or in other words, a diameter. In essence, one can imagine that the volume literally occupied by the particle traveling through space is a cylinder with a length equal to the free path and a radius equal to the particle's diameter.
ID:(1962, 0)
Mean free path for moving neighbors
Equation
For the case without movement, the probability is the free path ($\bar{l}$), whereas with movement, the probabilities are the particle diameter ($d$) and the particle concentration ($c_n$), respectively.
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
In the case of movement, the probability increases by a factor of $\sqrt{2}$, which means the free path is
 $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)