Utilizador:
Princípio da lei da alavanca
Descrição 
Uma vez que o torque gerado pela força gravitacional e pelo braço da alavanca é
| $ T = r F $ |
em cada lado da balança, no caso de equilíbrio, ele deve se anular para que haja equilíbrio:
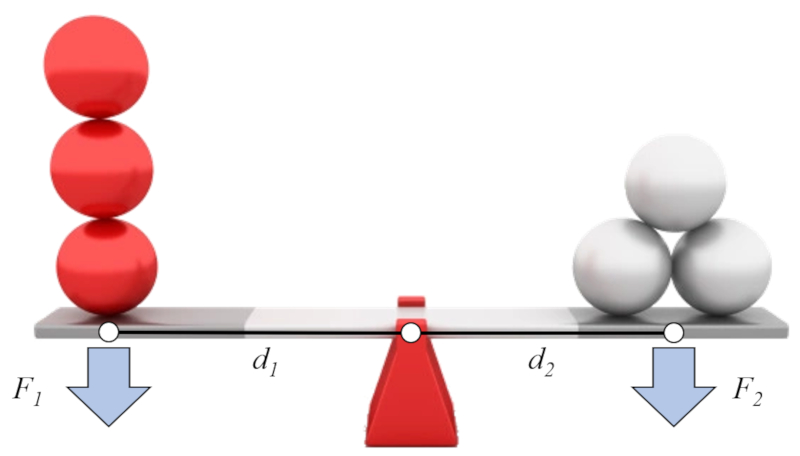
Se assumirmos que de um lado temos la força 1 ($F_1$) e la força de distância - veio (braço) 1 ($d_1$), e do outro lado la força 2 ($F_2$) e la força de distância - veio (braço) 2 ($d_2$), podemos estabelecer a chamada lei da alavanca da seguinte forma:
| $ d_1 F_1 = d_2 F_2 $ |
 $$ |
ID:(15847, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ d_1 F_1 = d_2 F_2 $
d_1 * F_1 = d_2 * F_2
$ F_1 = m_1 g $
F_g = m_g * g
$ F_2 = m_2 g $
F_g = m_g * g
$ T_1 = d_1 F_1 $
T = r * F
$ T_2 = d_2 F_2 $
T = r * F
ID:(15846, 0)
Lei da Alavanca
Equação
Se uma barra montada em um ponto que atua como eixo for submetida a la força 1 ($F_1$) em la força de distância - veio (braço) 1 ($d_1$) do eixo, gerando um torque $T_1$, e a la força 2 ($F_2$) em la força de distância - veio (braço) 2 ($d_2$) do eixo, gerando um torque $T_2$, ela estará em equilíbrio se ambos os torques forem iguais. Portanto, o equilíbrio corresponde à chamada lei da alavanca, expressa como:
| $ d_1 F_1 = d_2 F_2 $ |
No caso de uma balança, atua sobre cada braço uma força gravitacional que gera um torque
| $ T = r F $ |
Se o comprimento dos braços for $d_i$ e as forças forem $F_i$ com $i=1,2$, a condição de equilíbrio exige que a soma dos torques seja zero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Portanto, considerando que o sinal de cada torque depende da direção em que está induzindo a rotação,
$d_1F_1-d_2F_2=0$
o que resulta em
| $ d_1 F_1 = d_2 F_2 $ |
.
ID:(3250, 0)
Torque simples - relação de força (1)
Equação
Dado que a relação entre o momento angular e o torque é
| $ L = r p $ |
sua derivada temporal nos leva à relação do torque
| $ T_1 = d_1 F_1 $ |
| $ T = r F $ |
A rotação do corpo ocorre em torno de um eixo na direção do torque, que passa pelo centro de massa.
ID:(4431, 1)
Torque simples - relação de força (2)
Equação
Dado que a relação entre o momento angular e o torque é
| $ L = r p $ |
sua derivada temporal nos leva à relação do torque
| $ T_2 = d_2 F_2 $ |
| $ T = r F $ |
A rotação do corpo ocorre em torno de um eixo na direção do torque, que passa pelo centro de massa.
ID:(4431, 2)
Força gravitacional (1)
Equação
La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superfície do planeta. Esta última é identificada por la aceleração gravitacional ($g$), que é igual a $9.8 m/s^2$.
Consequentemente, conclui-se que:
| $ F_1 = m_1 g $ |
| $ F_g = m_g g $ |
ID:(3241, 1)
Força gravitacional (2)
Equação
La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superfície do planeta. Esta última é identificada por la aceleração gravitacional ($g$), que é igual a $9.8 m/s^2$.
Consequentemente, conclui-se que:
| $ F_2 = m_2 g $ |
| $ F_g = m_g g $ |
ID:(3241, 2)