User:
Principle of Lever's Law
Description 
Since the torque generated by the gravitational force and the lever arm is
| $ T = r F $ |
on each side of the balance, it must cancel out in the case of equilibrium to achieve balance:
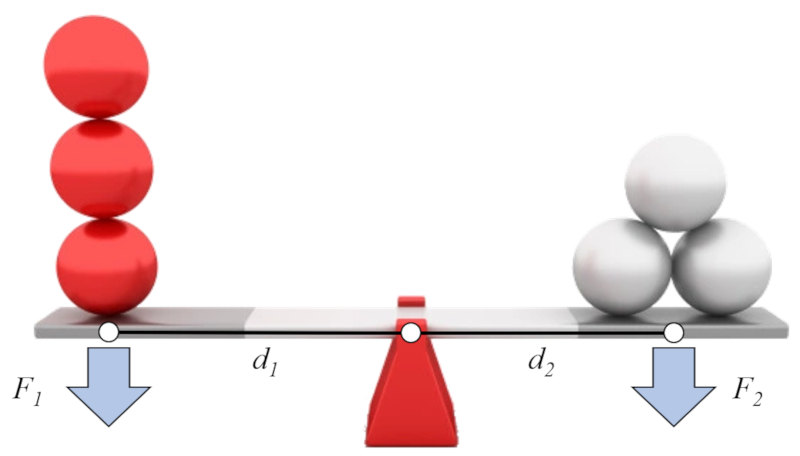
If we assume that on one side we have the force 1 ($F_1$) and the force - axis distance (arm) 1 ($d_1$), and on the other side the force 2 ($F_2$) and the force - axis distance (arm) 2 ($d_2$), we can establish the well-known lever law as follows:
| $ d_1 F_1 = d_2 F_2 $ |
ID:(15847, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ d_1 F_1 = d_2 F_2 $
d_1 * F_1 = d_2 * F_2
$ F_1 = m_1 g $
F_g = m_g * g
$ F_2 = m_2 g $
F_g = m_g * g
$ T_1 = d_1 F_1 $
T = r * F
$ T_2 = d_2 F_2 $
T = r * F
ID:(15846, 0)
Lever Law
Equation
If a bar mounted on a point acting as a pivot is subjected to the force 1 ($F_1$) at the force - axis distance (arm) 1 ($d_1$) from the pivot, generating a torque $T_1$, and to the force 2 ($F_2$) at the force - axis distance (arm) 2 ($d_2$) from the pivot, generating a torque $T_2$, it will be in equilibrium if both torques are equal. Therefore, the equilibrium corresponds to the so-called law of the lever, expressed as:
| $ d_1 F_1 = d_2 F_2 $ |
In the case of a balance, a gravitational force acts on each arm, generating a torque
| $ T = r F $ |
If the lengths of the arms are $d_i$ and the forces are $F_i$ with $i=1,2$, the equilibrium condition requires that the sum of the torques be zero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Therefore, considering that the sign of each torque depends on the direction in which it induces rotation,
$d_1F_1-d_2F_2=0$
which results in
| $ d_1 F_1 = d_2 F_2 $ |
.
ID:(3250, 0)
Simple torque - force relationship (1)
Equation
Since the relationship between angular momentum and torque is
| $ L = r p $ |
its temporal derivative leads us to the torque relationship
| $ T_1 = d_1 F_1 $ |
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
The body's rotation occurs around an axis in the direction of the torque, which passes through the center of mass.
ID:(4431, 1)
Simple torque - force relationship (2)
Equation
Since the relationship between angular momentum and torque is
| $ L = r p $ |
its temporal derivative leads us to the torque relationship
| $ T_2 = d_2 F_2 $ |
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
The body's rotation occurs around an axis in the direction of the torque, which passes through the center of mass.
ID:(4431, 2)
Gravitational Force (1)
Equation
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_1 = m_1 g $ |
| $ F_g = m_g g $ |
ID:(3241, 1)
Gravitational Force (2)
Equation
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_2 = m_2 g $ |
| $ F_g = m_g g $ |
ID:(3241, 2)