Benützer:
Hebelgesetz
Storyboard 
Das Hebelgesetz entspricht einem System, das zwei gleichen und entgegengesetzten Drehmomenten ausgesetzt ist, mit denen das System im Gleichgewicht bleibt.
ID:(1457, 0)
Hebelgesetzprinzip
Beschreibung
Da das durch die Schwerkraft erzeugte Drehmoment und der Hebelarm
| $ T = r F $ |
auf jeder Seite der Waage vorhanden sind, muss es im Gleichgewichtszustand aufgehoben werden, um ein Gleichgewicht zu erreichen:
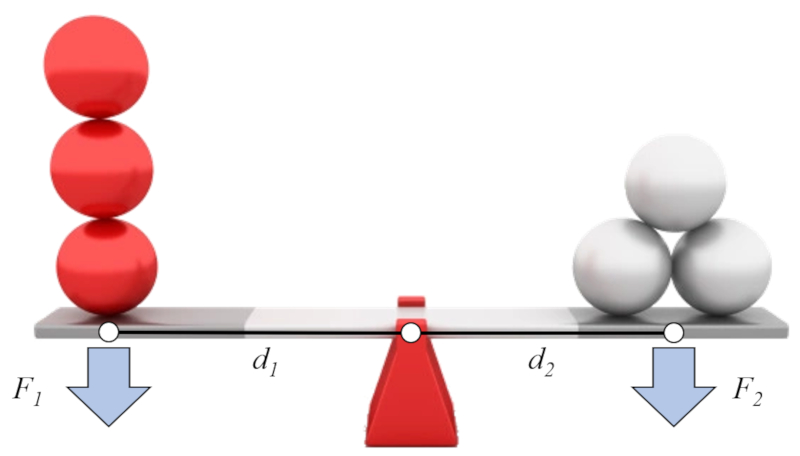
Wenn wir annehmen, dass auf der einen Seite die Kraft 1 ($F_1$) und der Abstand Kraft - Achse (Arm) 1 ($d_1$) und auf der anderen Seite die Kraft 2 ($F_2$) und der Abstand Kraft - Achse (Arm) 2 ($d_2$) vorhanden sind, kann das sogenannte Hebelgesetz wie folgt aufgestellt werden:
| $ d_1 F_1 = d_2 F_2 $ |
ID:(15847, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ d_1 F_1 = d_2 F_2 $
d_1 * F_1 = d_2 * F_2
$ F_1 = m_1 g $
F_g = m_g * g
$ F_2 = m_2 g $
F_g = m_g * g
$ T_1 = d_1 F_1 $
T = r * F
$ T_2 = d_2 F_2 $
T = r * F
ID:(15846, 0)
Hebelgesetz
Gleichung
Wenn eine Stange, die auf einem Punkt als Drehachse montiert ist, an die Kraft 1 ($F_1$) bei der Abstand Kraft - Achse (Arm) 1 ($d_1$) von der Achse ein Drehmoment $T_1$ erzeugt und an die Kraft 2 ($F_2$) bei der Abstand Kraft - Achse (Arm) 2 ($d_2$) ein Drehmoment $T_2$, dann ist sie im Gleichgewicht, wenn beide Drehmomente gleich sind. Das Gleichgewicht entspricht somit dem sogenannten Hebelgesetz, ausgedrückt als:
| $ d_1 F_1 = d_2 F_2 $ |
Im Falle einer Waage wirkt auf jeden Arm eine Gravitationskraft, die ein Drehmoment erzeugt
| $ T = r F $ |
Wenn die Längen der Arme $d_i$ betragen und die Kräfte $F_i$ mit $i=1,2$ sind, verlangt die Gleichgewichtsbedingung, dass die Summe der Drehmomente null ist:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Daher, unter Berücksichtigung, dass das Vorzeichen jedes Drehmoments von der Richtung abhängt, in der es eine Rotation induziert,
$d_1F_1-d_2F_2=0$
was zu
| $ d_1 F_1 = d_2 F_2 $ |
führt.
ID:(3250, 0)
Einfache Drehmoment-Kraft-Beziehung (1)
Gleichung
Da das Verhältnis zwischen dem Drehimpuls und dem Moment wie folgt ist:
| $ L = r p $ |
führt uns die zeitliche Ableitung zu der Beziehung des Drehmoments
| $ T_1 = d_1 F_1 $ |
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
Die Drehung des Körpers erfolgt um eine Achse in Richtung des Drehmoments, das durch den Schwerpunkt verläuft.
ID:(4431, 1)
Einfache Drehmoment-Kraft-Beziehung (2)
Gleichung
Da das Verhältnis zwischen dem Drehimpuls und dem Moment wie folgt ist:
| $ L = r p $ |
führt uns die zeitliche Ableitung zu der Beziehung des Drehmoments
| $ T_2 = d_2 F_2 $ |
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
Die Drehung des Körpers erfolgt um eine Achse in Richtung des Drehmoments, das durch den Schwerpunkt verläuft.
ID:(4431, 2)
Schwerkraft (1)
Gleichung
Die Schwerkraft ($F_g$) basiert auf die Gravitationsmasse ($m_g$) des Objekts und auf einer Konstanten, die die Intensität der Gravitation an der Oberfläche des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$) identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
| $ F_1 = m_1 g $ |
| $ F_g = m_g g $ |
ID:(3241, 1)
Schwerkraft (2)
Gleichung
Die Schwerkraft ($F_g$) basiert auf die Gravitationsmasse ($m_g$) des Objekts und auf einer Konstanten, die die Intensität der Gravitation an der Oberfläche des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$) identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
| $ F_2 = m_2 g $ |
| $ F_g = m_g g $ |
ID:(3241, 2)