Usuario:
Ley de Palanca
Storyboard 
La ley de palanca corresponde a un sistema expuesto a dos torques iguales y opuestos con lo que el sistema queda en equilibrio.
ID:(1457, 0)
Principio de la ley de Palanca
Descripción
Dado que el torque generado por la fuerza gravitacional y el brazo es
| $ T = r F $ |
en cada lado de la balanza, en caso de equilibrio debe anularse para que exista un estado de equilibrio:
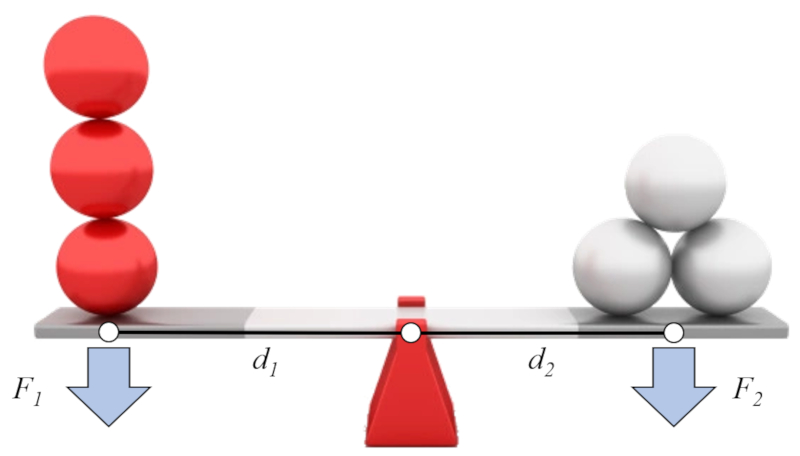
Si asumimos que por un lado se tienen la fuerza 1 ($F_1$) y el distancia fuerza - eje (brazo) 1 ($d_1$), y por el otro lado la fuerza 2 ($F_2$) y el distancia fuerza - eje (brazo) 2 ($d_2$), se puede formular la conocida ley de la palanca de la siguiente manera:
| $ d_1 F_1 = d_2 F_2 $ |
ID:(15847, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ d_1 F_1 = d_2 F_2 $
d_1 * F_1 = d_2 * F_2
$ F_1 = m_1 g $
F_g = m_g * g
$ F_2 = m_2 g $
F_g = m_g * g
$ T_1 = d_1 F_1 $
T = r * F
$ T_2 = d_2 F_2 $
T = r * F
ID:(15846, 0)
Ley de Palanca
Ecuación
Si una barra montada sobre un punto que actúa como eje es sometida a la fuerza 1 ($F_1$) a el distancia fuerza - eje (brazo) 1 ($d_1$) del eje, generando un torque $T_1$, y a la fuerza 2 ($F_2$) a el distancia fuerza - eje (brazo) 2 ($d_2$) del eje, generando un torque $T_2$, estará en equilibrio cuando ambos torques sean iguales. Por lo tanto, el equilibrio se describe mediante la llamada ley de la palanca, expresada como:
| $ d_1 F_1 = d_2 F_2 $ |
En el caso de una balanza, actúa una fuerza gravitacional sobre cada brazo que genera un torque
| $ T = r F $ |
Si la longitud de los brazos es $d_i$ y las fuerzas son $F_i$ con $i=1,2$, la condición de equilibrio exige que la suma de los torques sea cero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Por lo tanto, considerando que el signo de cada torque depende de la dirección en la que está induciendo el giro,
$d_1F_1-d_2F_2=0$
de lo que resulta
| $ d_1 F_1 = d_2 F_2 $ |
.
ID:(3250, 0)
Relación simple torque - fuerza (1)
Ecuación
Dado que la relación entre el momento angular y el momento es
| $ L = r p $ |
su derivada temporal nos conduce a la relación de torque
| $ T_1 = d_1 F_1 $ |
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
La rotación del cuerpo tiene lugar alrededor de un eje en la dirección del torque, que atraviesa el centro de masa.
ID:(4431, 1)
Relación simple torque - fuerza (2)
Ecuación
Dado que la relación entre el momento angular y el momento es
| $ L = r p $ |
su derivada temporal nos conduce a la relación de torque
| $ T_2 = d_2 F_2 $ |
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
La rotación del cuerpo tiene lugar alrededor de un eje en la dirección del torque, que atraviesa el centro de masa.
ID:(4431, 2)
Fuerza gravitacional (1)
Ecuación
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta última es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
| $ F_1 = m_1 g $ |
| $ F_g = m_g g $ |
ID:(3241, 1)
Fuerza gravitacional (2)
Ecuación
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta última es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
| $ F_2 = m_2 g $ |
| $ F_g = m_g g $ |
ID:(3241, 2)