Utilisateur:
Principe de la loi du levier
Description 
Étant donné que le couple généré par la force gravitationnelle et le bras de levier est
| $ T = r F $ |
de chaque côté de la balance, il doit s'annuler en cas d'équilibre pour atteindre l'équilibre :
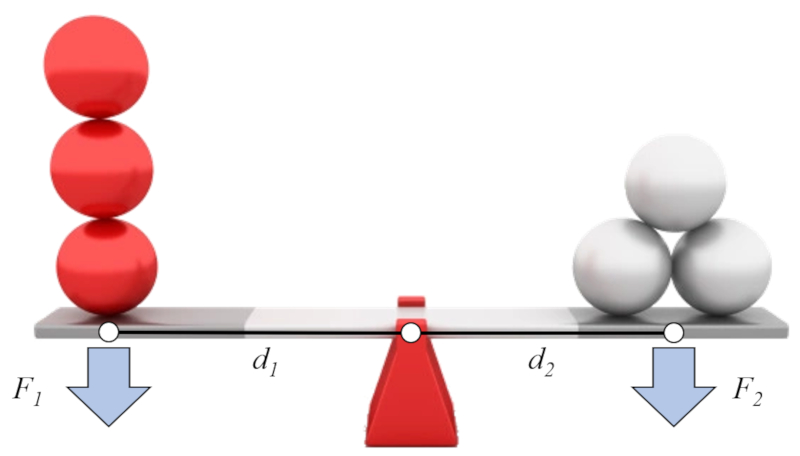
Si l'on suppose que d'un côté, nous avons a forcer 1 ($F_1$) et a force de distance - axe (bras) 1 ($d_1$), et de l'autre côté A forcer 2 ($F_2$) et a force de distance - axe (bras) 2 ($d_2$), on peut établir la loi dite du levier comme suit :
| $ d_1 F_1 = d_2 F_2 $ |
ID:(15847, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ d_1 F_1 = d_2 F_2 $
d_1 * F_1 = d_2 * F_2
$ F_1 = m_1 g $
F_g = m_g * g
$ F_2 = m_2 g $
F_g = m_g * g
$ T_1 = d_1 F_1 $
T = r * F
$ T_2 = d_2 F_2 $
T = r * F
ID:(15846, 0)
Loi du levier
Équation
Si une barre montée sur un point servant d'axe est soumise à A forcer 1 ($F_1$) à A force de distance - axe (bras) 1 ($d_1$) de l'axe, générant un couple $T_1$, et à A forcer 2 ($F_2$) à A force de distance - axe (bras) 2 ($d_2$) de l'axe, générant un couple $T_2$, elle sera en équilibre si les deux couples sont égaux. Ainsi, l'équilibre correspond à la loi du levier, exprimée comme suit :
| $ d_1 F_1 = d_2 F_2 $ |
Dans le cas d'une balance, une force gravitationnelle agit sur chaque bras, générant un couple
| $ T = r F $ |
Si les longueurs des bras sont $d_i$ et les forces sont $F_i$ avec $i=1,2$, la condition d'équilibre exige que la somme des couples soit nulle :
| $\displaystyle\sum_i \vec{T}_i=0$ |
Par conséquent, en considérant que le signe de chaque couple dépend de la direction dans laquelle il induit une rotation,
$d_1F_1-d_2F_2=0$
ce qui donne comme résultat
.
ID:(3250, 0)
Relation simple couple - force (1)
Équation
Puisque la relation entre le moment angulaire et le moment est
| $ L = r p $ |
sa dérivée temporelle nous conduit à la relation du moment de force
| $ T_1 = d_1 F_1 $ |
| $ T = r F $ |
La rotation du corps se produit autour d'un axe dans la direction du moment de force, qui passe par le centre de masse.
ID:(4431, 1)
Relation simple couple - force (2)
Équation
Puisque la relation entre le moment angulaire et le moment est
| $ L = r p $ |
sa dérivée temporelle nous conduit à la relation du moment de force
| $ T_2 = d_2 F_2 $ |
| $ T = r F $ |
La rotation du corps se produit autour d'un axe dans la direction du moment de force, qui passe par le centre de masse.
ID:(4431, 2)
Force gravitationnelle (1)
Équation
A force gravitationnelle ($F_g$) est basé sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui reflète l'intensité de la gravité à la surface de la planète. Cette dernière est identifiée par a accélération gravitationnelle ($g$), qui est égal à $9.8 m/s^2$.
Par conséquent, on en conclut que :
| $ F_1 = m_1 g $ |
| $ F_g = m_g g $ |
ID:(3241, 1)
Force gravitationnelle (2)
Équation
A force gravitationnelle ($F_g$) est basé sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui reflète l'intensité de la gravité à la surface de la planète. Cette dernière est identifiée par a accélération gravitationnelle ($g$), qui est égal à $9.8 m/s^2$.
Par conséquent, on en conclut que :
| $ F_2 = m_2 g $ |
| $ F_g = m_g g $ |
ID:(3241, 2)