Storyboard

Es gibt verschiedene Arten von Oszillatoren, wobei die meist diskutierten durch eine Feder und das Pendel geschlossen werden. Beide sind relevant, um zu untersuchen, wie wir gehen.

Einerseits gibt es das Verhalten einer Feder, das die Muskeln zeigen können. Andererseits gibt es beim Bewegen Systeme wie Arme, die Ausgleichsarbeit leisten und mit der gleichen Frequenz unserer Schritte oszillieren.

Beim Pendel gibt es zwei Arten: den Mathematiker, der die Schwingung einer Punktmasse betrachtet, und den Physiker, der die Form des Objekts als solche betrachtet.

>Modell

ID:(51, 0)

Gleichung

>Top, >Modell

En el caso de un resorte la energía total E_k, que se conserva, esta conformada por la energía cinética

donde m_i es la masa y v la velocidad, y la energía potencial elástica del resorte

\\n\\ndonde k es la constante del resorte y x la elongación, de la forma\\n\\n

$E_k=\displaystyle\frac{1}{2}m_iv^2+\displaystyle\frac{1}{2}kx^2$

Si uno reescribe esta expresión como

$\displaystyle\frac{ v ^2}{\displaystyle\frac{2 E }{ m_i }}+\displaystyle\frac{ x ^2}{\displaystyle\frac{2 E }{ k }}=1$

Bedingungen

Variablen

$E$

Energía del resorte

$J$

9787

$k$

Hookes Konstante

$N/m$

5311

$x$

Posición (vector)

$m$

9773

$m_i$

Träge Masse

$kg$

6290

$v$

Velocidad del resorte

$m/s$

9769

Beziehung

\\n\\nse puede dar cuenta que corresponde a una elipse en el espacio velocidad v y elongación x, con los semiejes\\n\\n

$a=\sqrt{\displaystyle\frac{2E_k}{k}}=x_0$

, y\\n\\n

$b=\sqrt{\displaystyle\frac{2E_k}{m_i}}=v_0$

.

Los semiejes corresponde a la vez a la velocidad v_0 y amplitud x_0 máximas respectivamente.

ID:(7101, 0)

Beschreibung

>Top

En el espacio de fase la oscilación se puede representar por una elipse

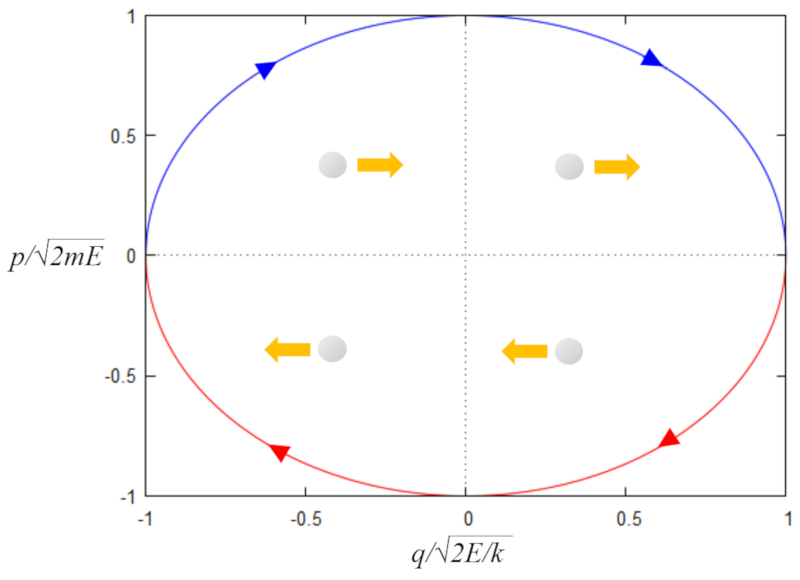
\\n \\nque en forma matemática se escribe como\\n\\n

$\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1$

\\n\\nde semiejes a y b se puede representar mediante un parámetro u que va de 0 a 2\pi mediante dos funciones trigonométricas\\n\\n

$x=a\cos u$

\\n\\ny\\n\\n

$y=b\sin u$

ID:(7105, 0)

Gleichung

>Top, >Modell

En el caso de la amplitud, que corresponde a nuestra coordenada x se tiene que el semieje es\\n\\n

$a=\sqrt{\displaystyle\frac{2E_k}{k}}$

\\n\\ny el tiempo se escala como\\n\\n

$u=\displaystyle\frac{2\pi t}{T}$

por lo que la amplitud será con igual a

$x =\sqrt{\displaystyle\frac{2 E }{ k }}\cos \displaystyle\frac{2 \pi t }{ T }$

Bedingungen

Variablen

$E$

Energía del resorte

$J$

9787

$k$

Hookes Konstante

$N/m$

5311

$\pi$

Pi

3.1415927

$rad$

5057

$x$

Posición (vector)

$m$

9773

$T$

Zeit

$s$

5078

$t$

Zeit

$s$

5264

Beziehung

ID:(7102, 0)

Gleichung

>Top, >Modell

En el caso de la velocidad, que corresponde a nuestra coordenada y se tiene que el semieje es\\n\\n

$b=\sqrt{\displaystyle\frac{2E}{m}}$

\\n\\ny el tiempo se escala como\\n\\n

$u=\displaystyle\frac{2\pi t}{T}$

por lo que la velocidad será igual a

$v =-\sqrt{\displaystyle\frac{2 E }{ m_i }}\sin \displaystyle\frac{2 \pi t }{ T }$

Bedingungen

Variablen

$E$

Energía del resorte

$J$

9787

$v$

Geschwindigkeit

$m/s$

6029

$\pi$

Pi

3.1415927

$rad$

5057

$m_i$

Träge Masse

$kg$

6290

$T$

Zeit

$s$

5078

$t$

Zeit

$s$

5264

Beziehung

ID:(7104, 0)

Gleichung

>Top, >Modell

Como la oscilación cumple las leyes físicas se puede hacer uso del hecho que el area debajo de la curva velocidad vs tiempo el camino recorrido para determinar el perido. Como la velocidad es\\n\\n

$\displaystyle\int_0^{T/2}v(t)dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\int_0^{T/2}\cos \displaystyle\frac{2\pi t}{T}dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\frac{T}{\pi}$

\\n\\ny el camino entre un mínimo a un máximo de una elongación, lo que ocurre entre el tiempo 0 y T/2 es igual a\\n\\n

$x_{max}-x_{min}=2\sqrt{\displaystyle\frac{2E}{k}}$

se tiene que

$T =2 \pi \sqrt{\displaystyle\frac{ m_i }{ k }}$

Bedingungen

Variablen

$k$

Hookes Konstante

$N/m$

5311

$\pi$

Pi

3.1415927

$rad$

5057

$m_i$

Träge Masse

$kg$

6290

$T$

Zeit

$s$

5078

Beziehung

ID:(7106, 0)

Gleichung

>Top, >Modell

Die Frequenz ($\nu$) entspricht der Anzahl der Schwingungen, die innerhalb einer Sekunde auftreten. Die Zeit ($T$) repräsentiert die Zeit, die für eine einzelne Schwingung benötigt wird. Daher ist die Anzahl der Schwingungen pro Sekunde:

$\nu =\displaystyle\frac{1}{ T }$

Bedingungen

Variablen

$\nu$

Frequenz

$Hz$

5077

$T$

Zeit

$s$

5078

Beziehung

Die Frequenz wird in Hertz (Hz) angegeben.

ID:(4427, 0)

Gleichung

>Top, >Modell

Como la frecuencia angular es con igual a

y la frecuencia con frequenz $Hz$ und zeit $s$ igual a

se tiene que con frequenz $Hz$ und zeit $s$ igual a

$\omega = 2 \pi \nu$

Bedingungen

Variablen

$\nu$

Frequenz

$Hz$

5077

$\pi$

Pi

3.1415927

$rad$

5057

$\omega$

Winkelfrequenz

$rad/s$

9010

Beziehung

ID:(12338, 0)